Introductory talk on

Self-supervised learning and transformers

What is it and do I need it?


Julian C. Schäfer-Zimmermann


Max Planck Institute of Animal Behavior

Department for the Ecology of Animal Societies

Communication and Collective Movement (CoCoMo) Group


Self-supervised learning

The concepts

The concepts

There are multiple ways to learn from data


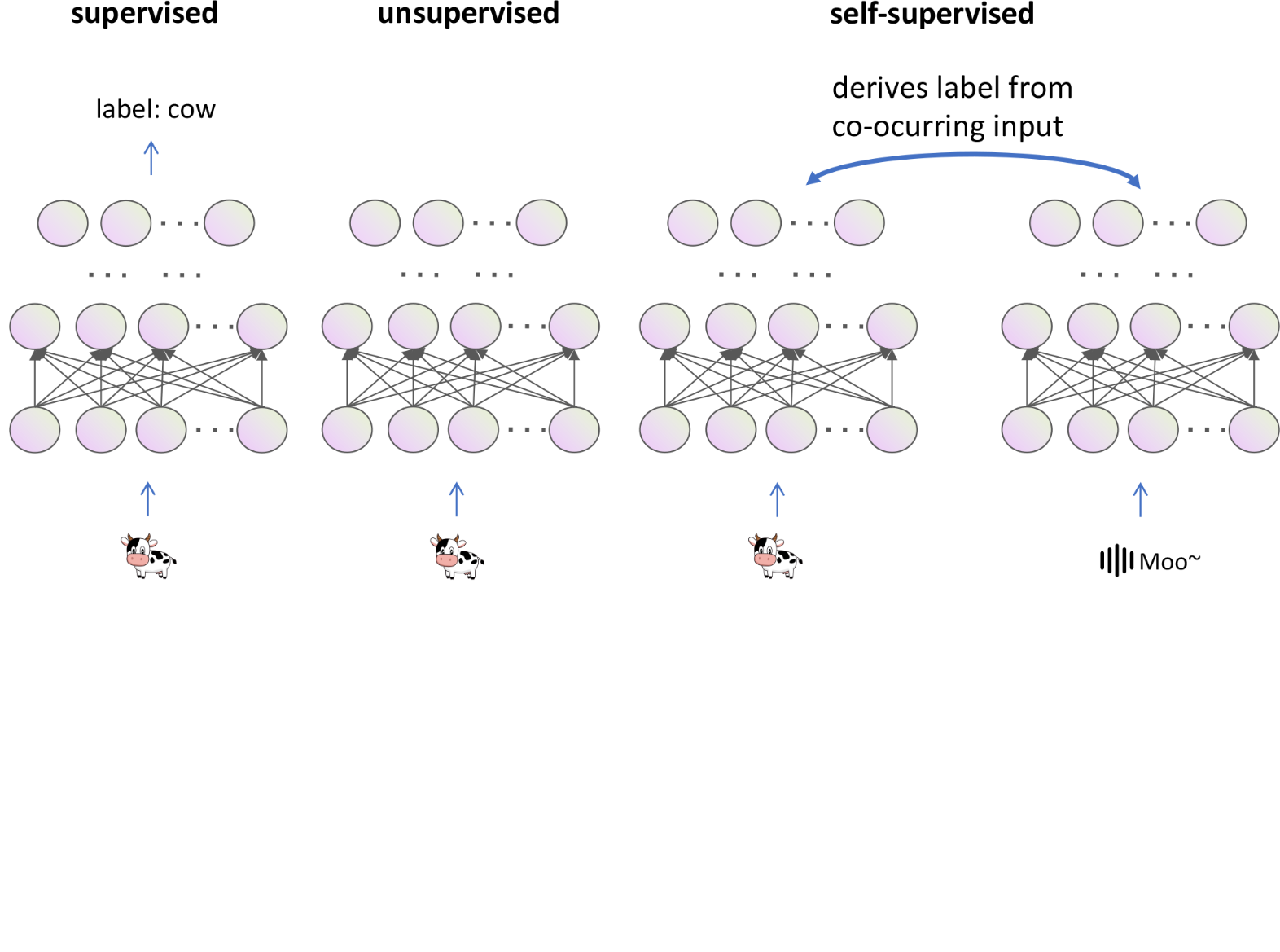
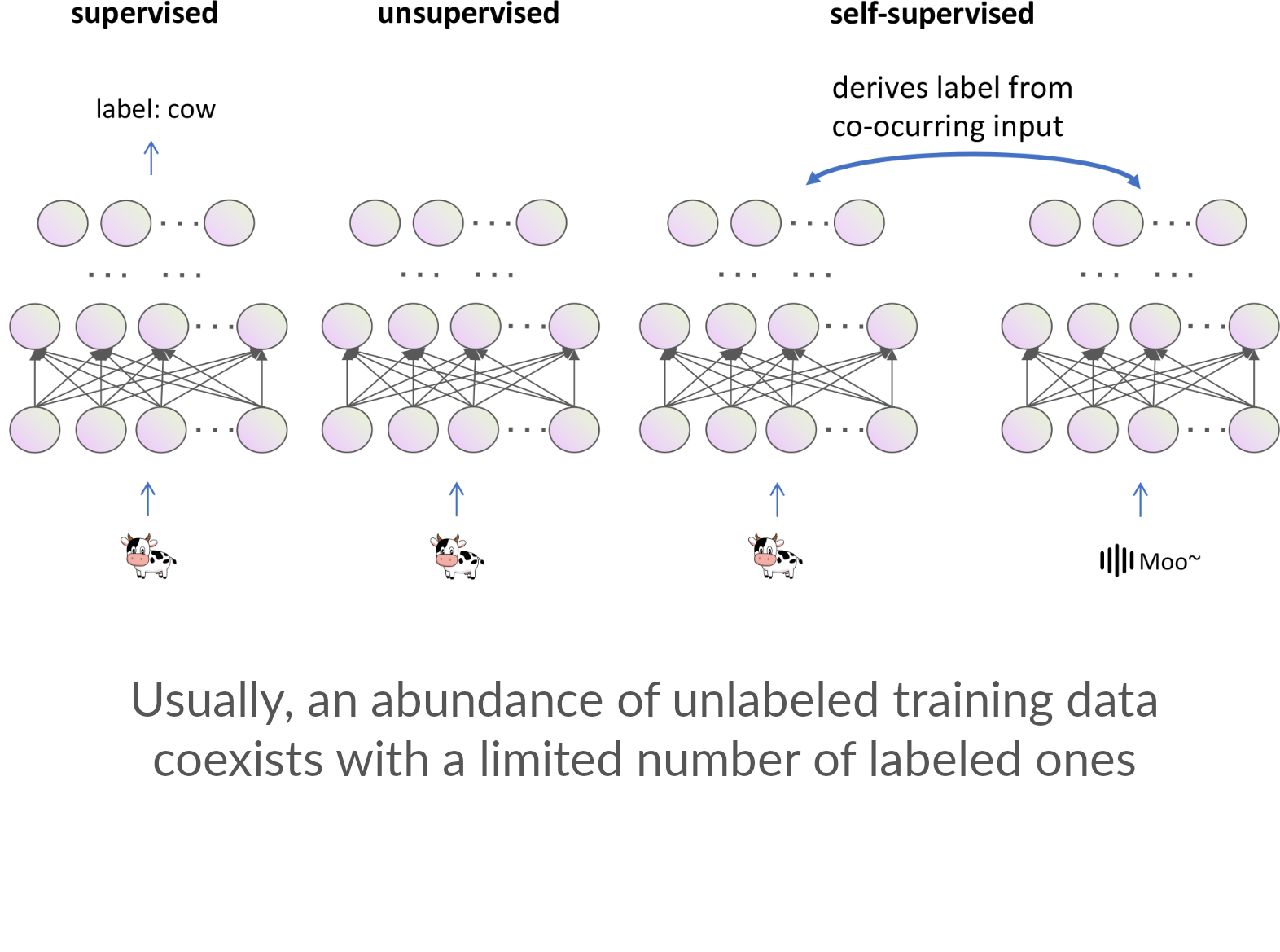
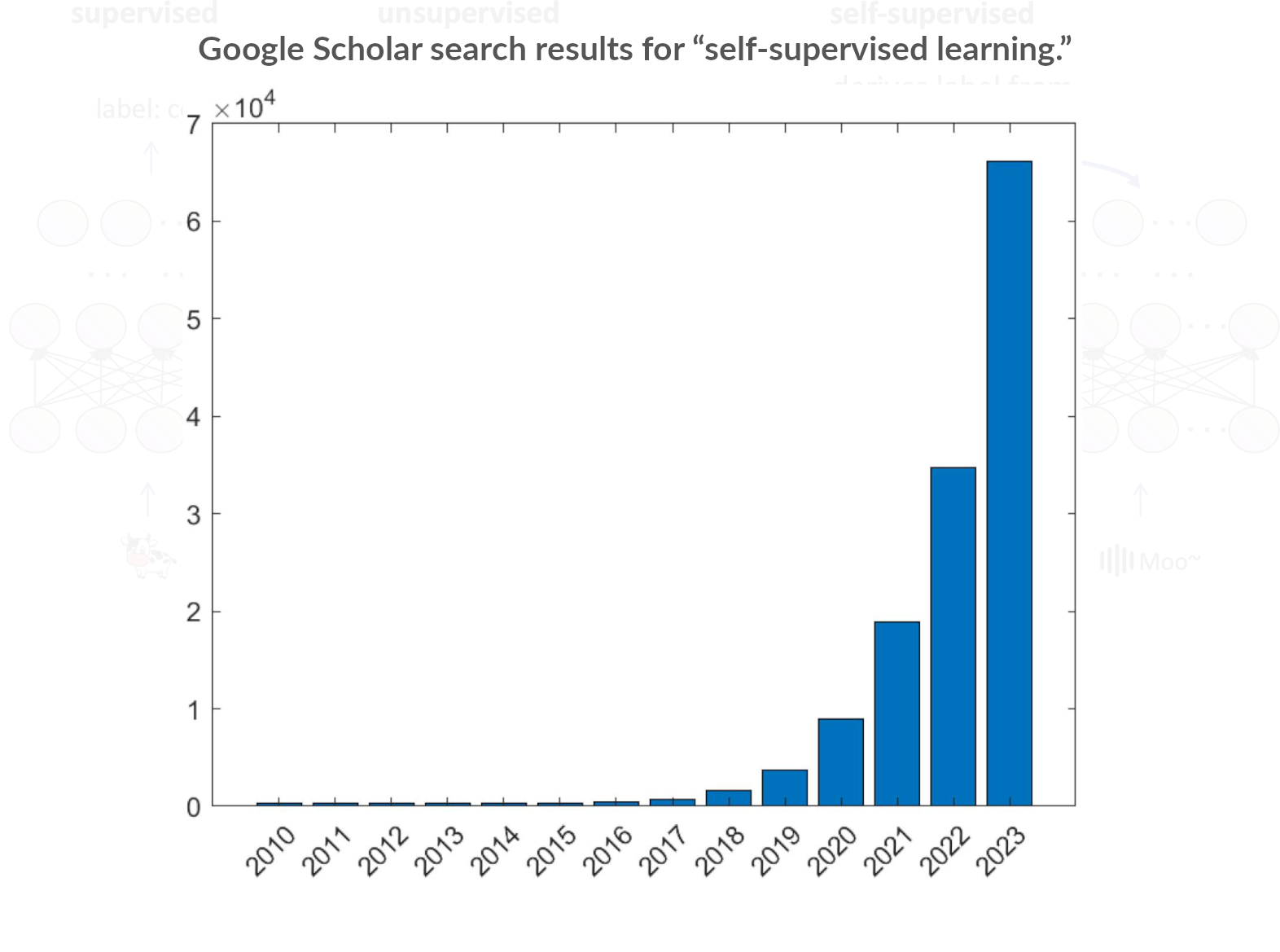
J. Gui et al. doi: 10.1109/TPAMI.2024.3415112 (2024)

The concepts

SSL is used as pretraining, followed by a finetuning step


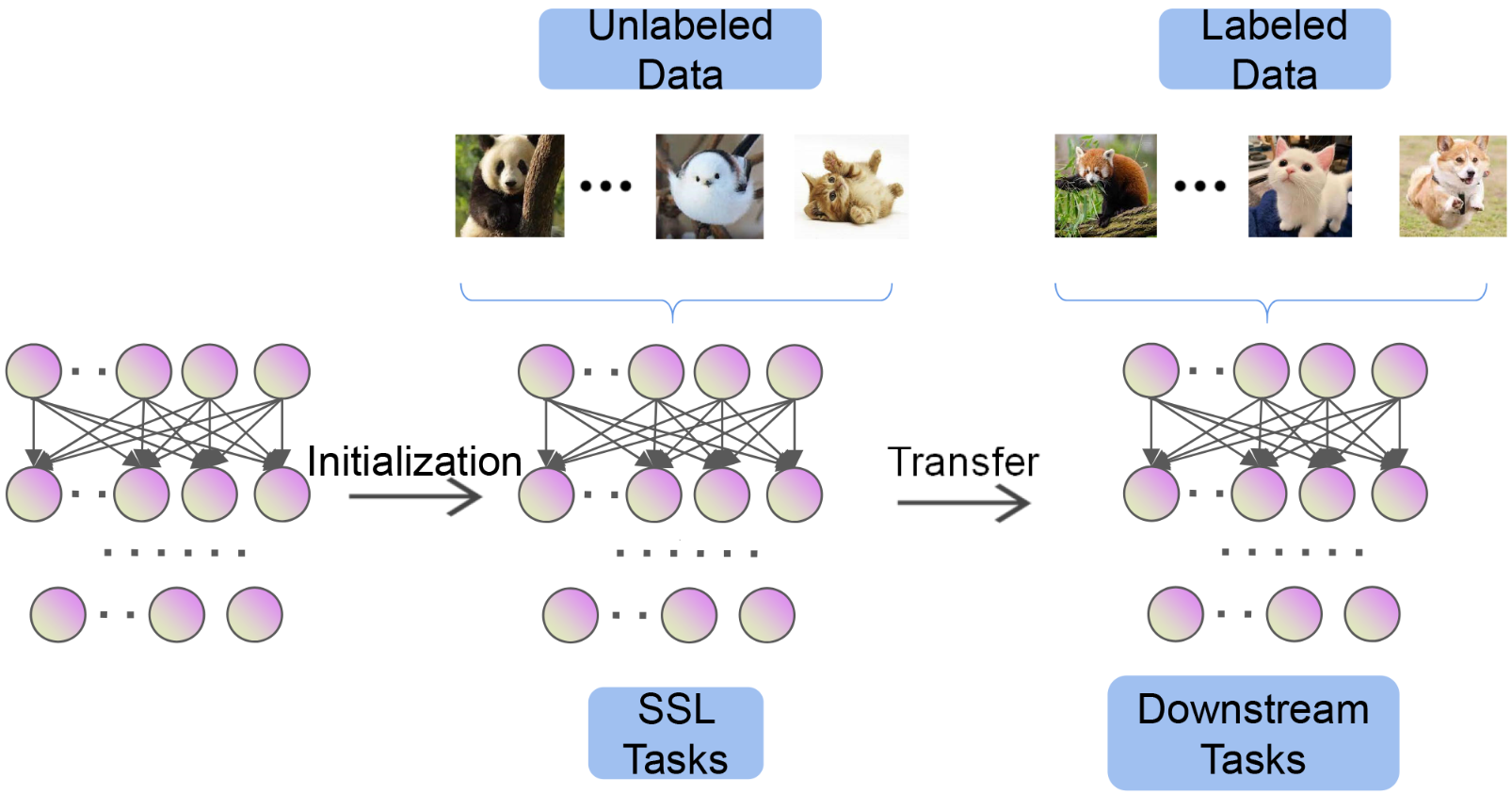
J. Gui et al. doi: 10.1109/TPAMI.2024.3415112 (2024)

The concepts

Predict everything from everything else


Meta Research Blog (March 4, 2021)

Self-supervised learning

Pretext tasks

Pretext tasks

Three categories


  • Context-based
  • Contrastive learning
  • Masked modeling

Pretext tasks

Context-based



Context-based methods rely on the inherent contextual relationships among the provided examples

J. Gui et al. doi: 10.1109/TPAMI.2024.3415112 (2024)

Pretext tasks

Contrastive learning



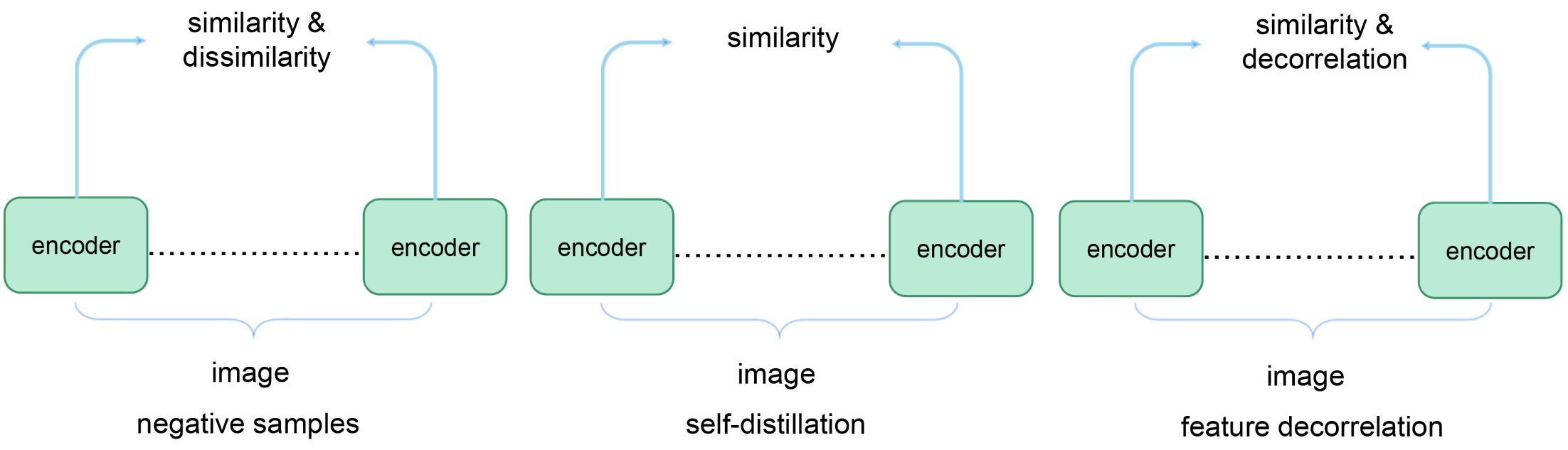
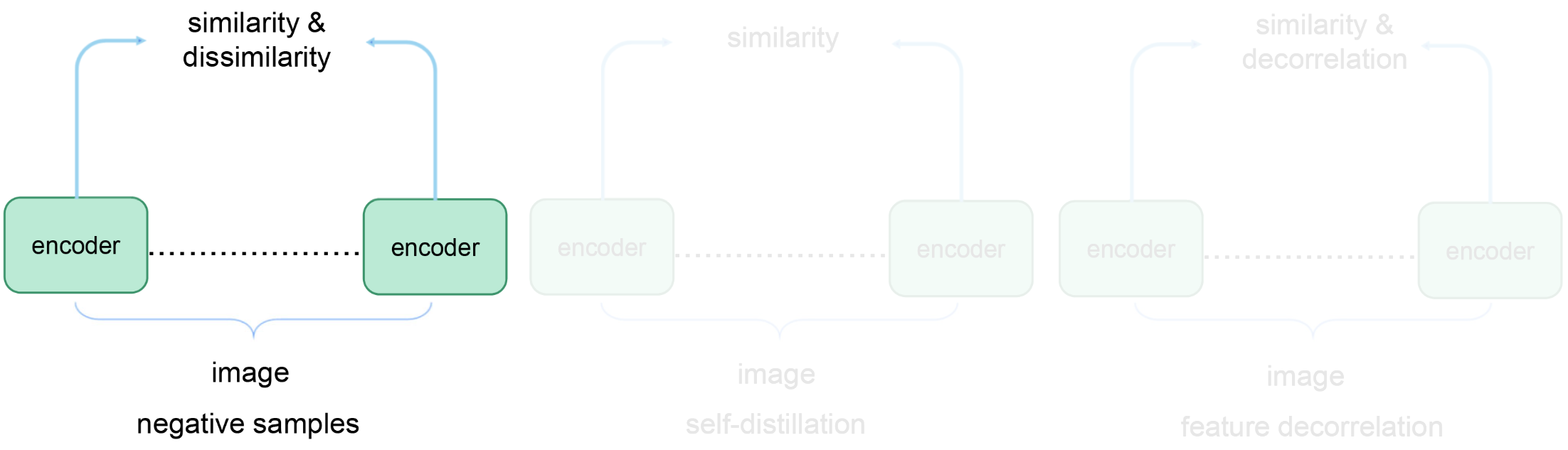
Contrastive learning is a discriminative tasks: Distinguish one instance from other ones

J. Gui et al. doi: 10.1109/TPAMI.2024.3415112 (2024)

Pretext tasks

Contrastive learning: Negative example-based


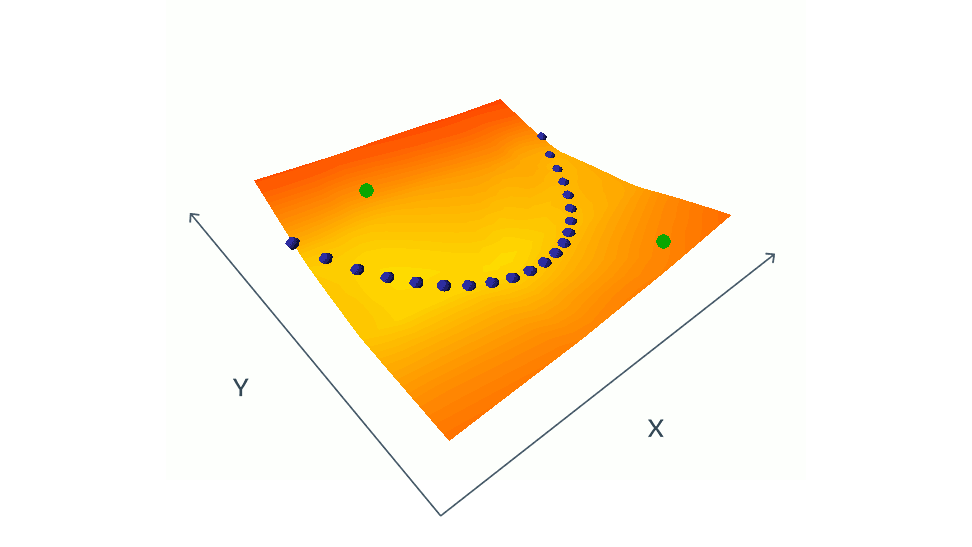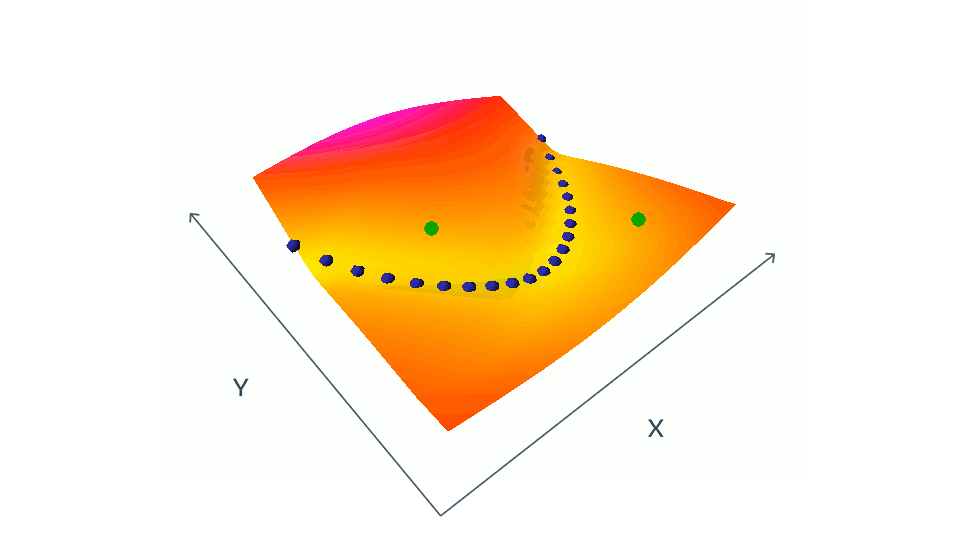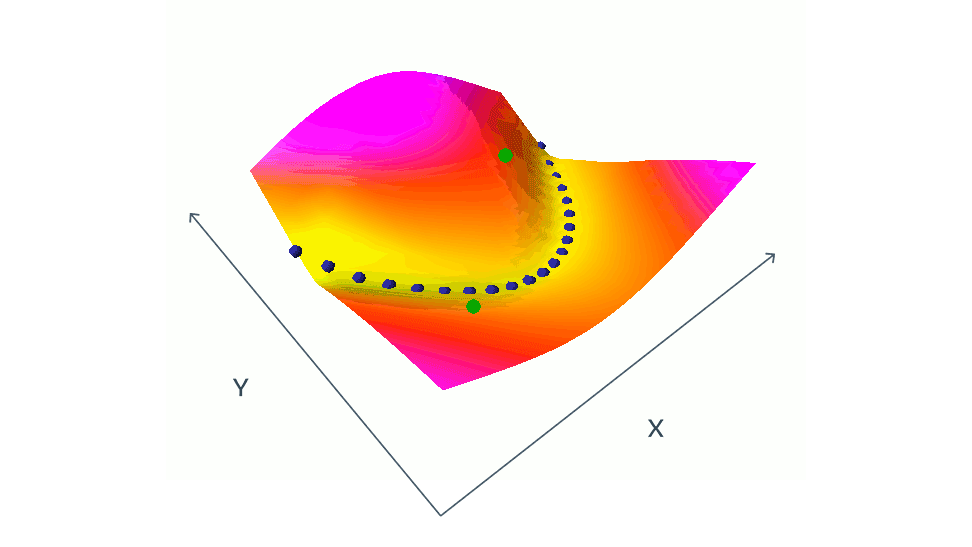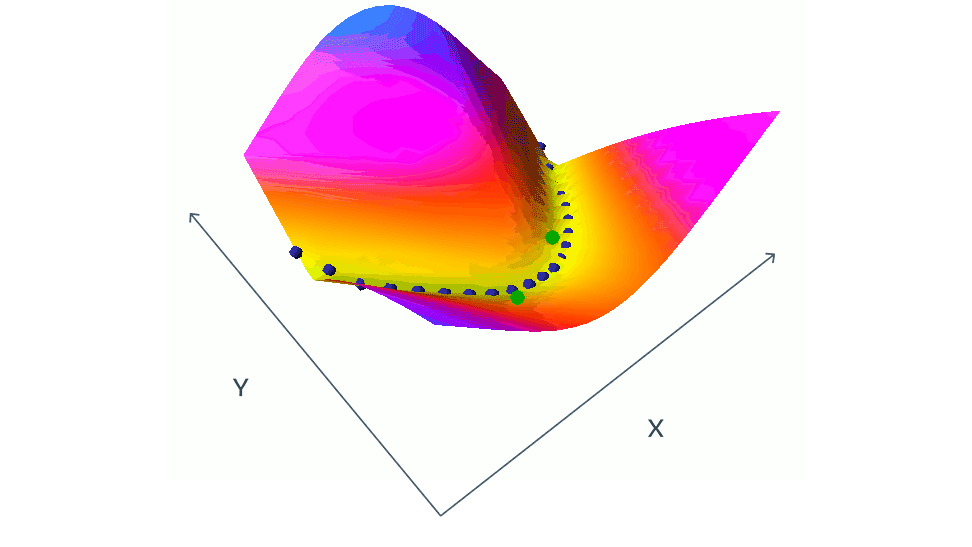
Negative example-based methods push down the loss of compatible pairs (blue dots), and push up on the loss of incompatible pairs (green dots)

Meta Research Blog (March 4, 2021)

Pretext tasks

Contrastive learning: Negative example-based


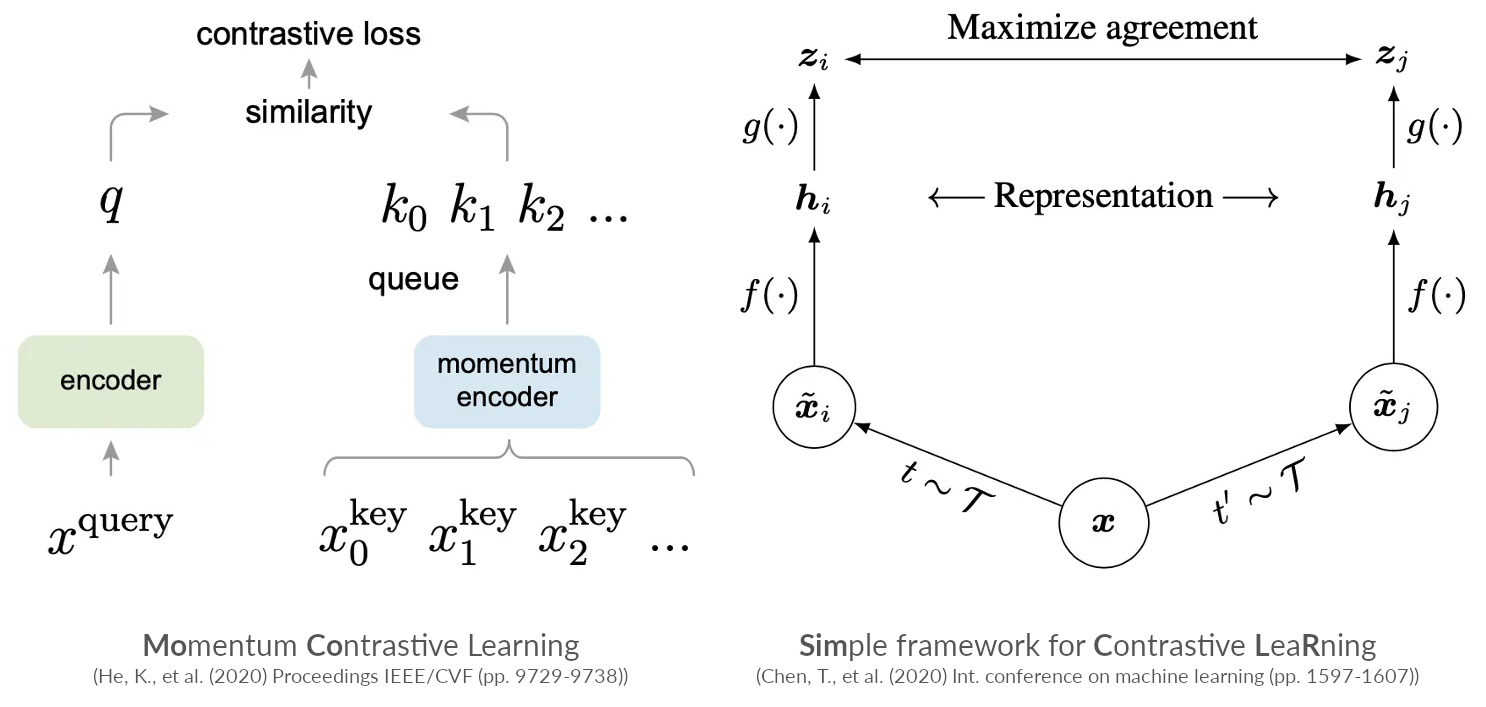
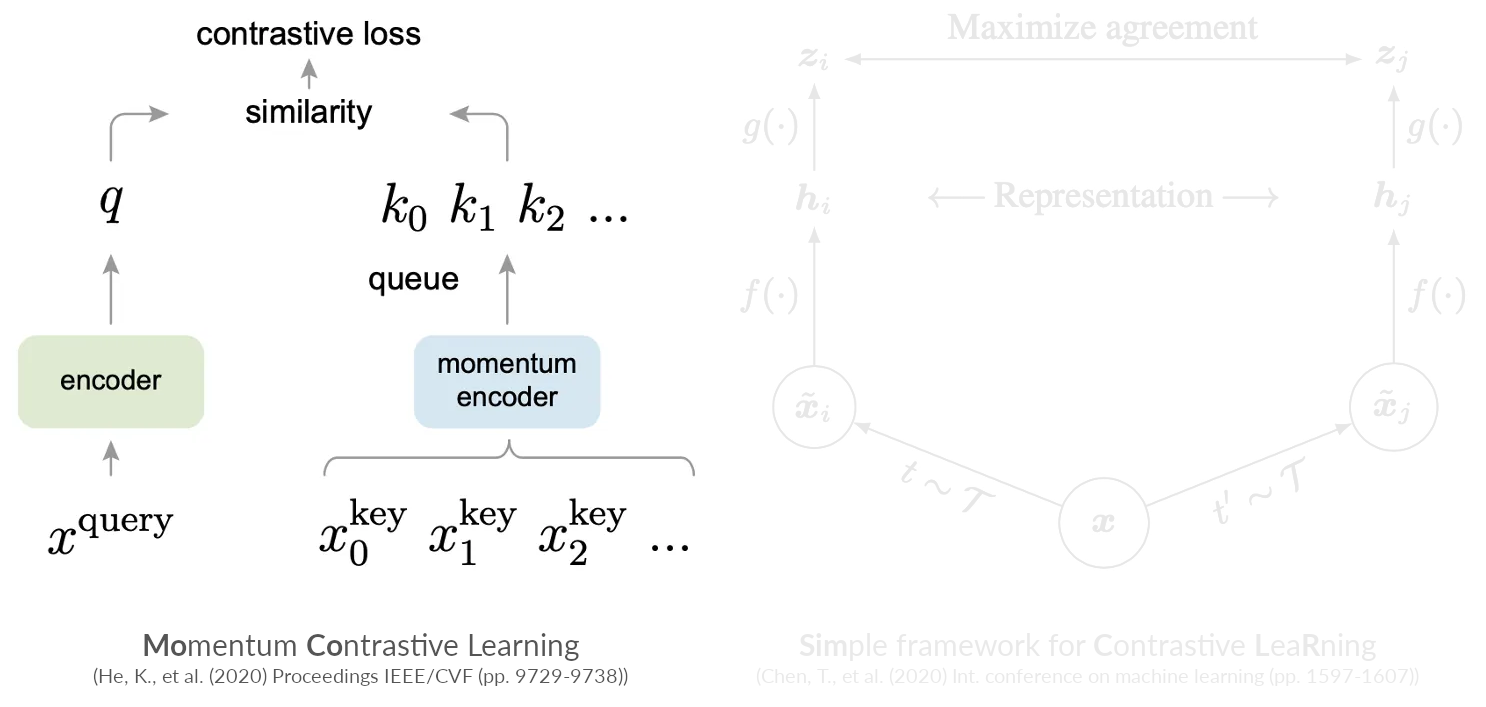
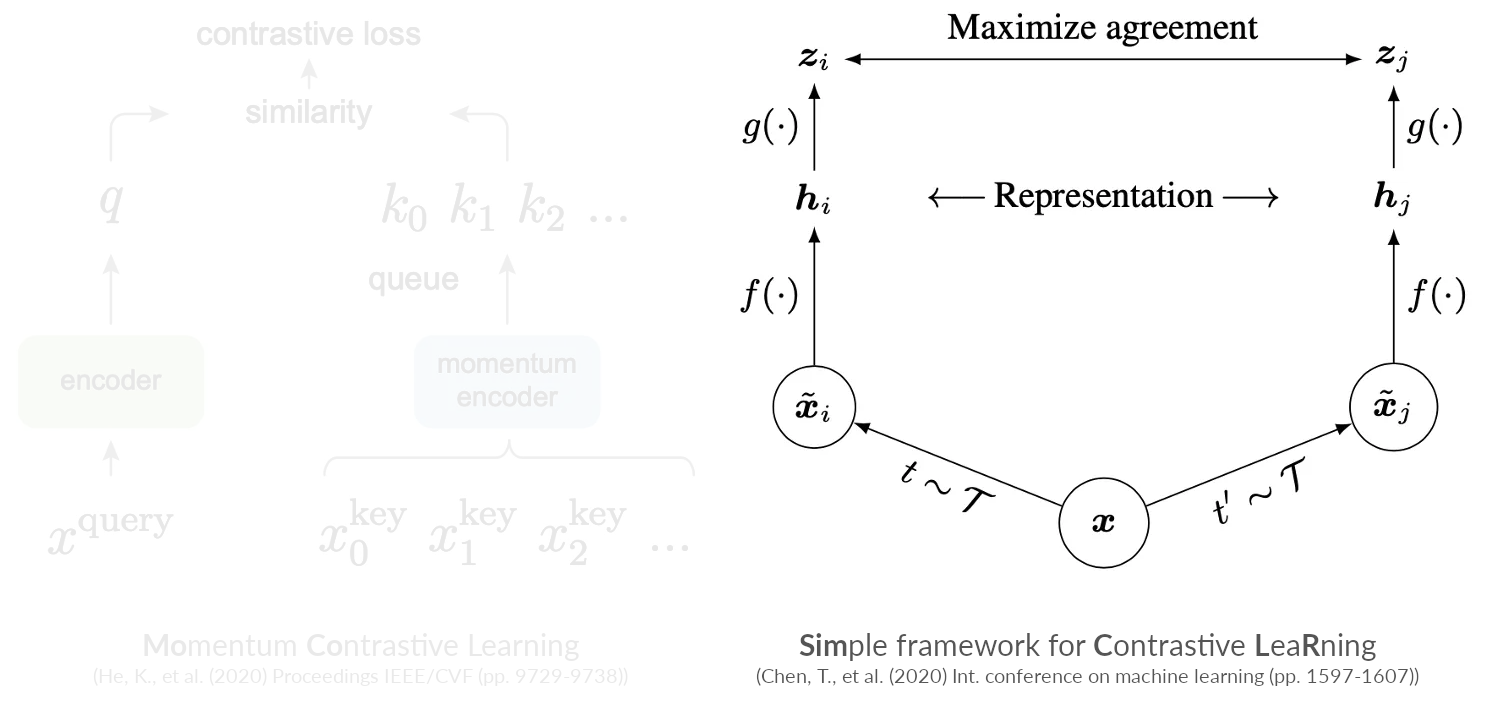
Pretext tasks

Contrastive learning


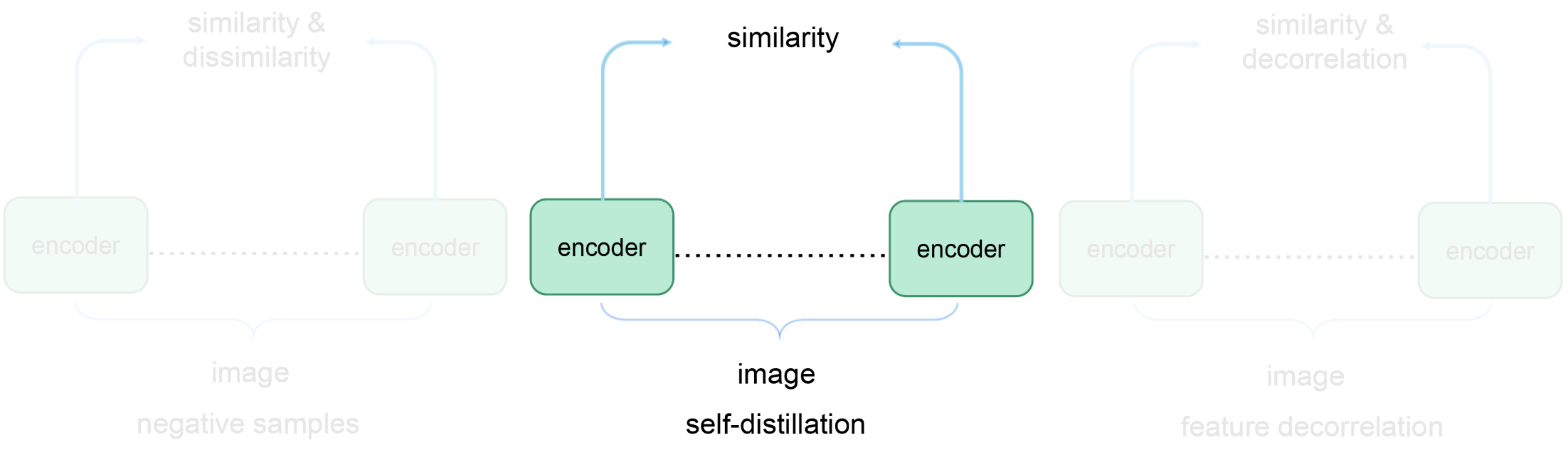
Pretext tasks

Contrastive learning: Self-distillation-based


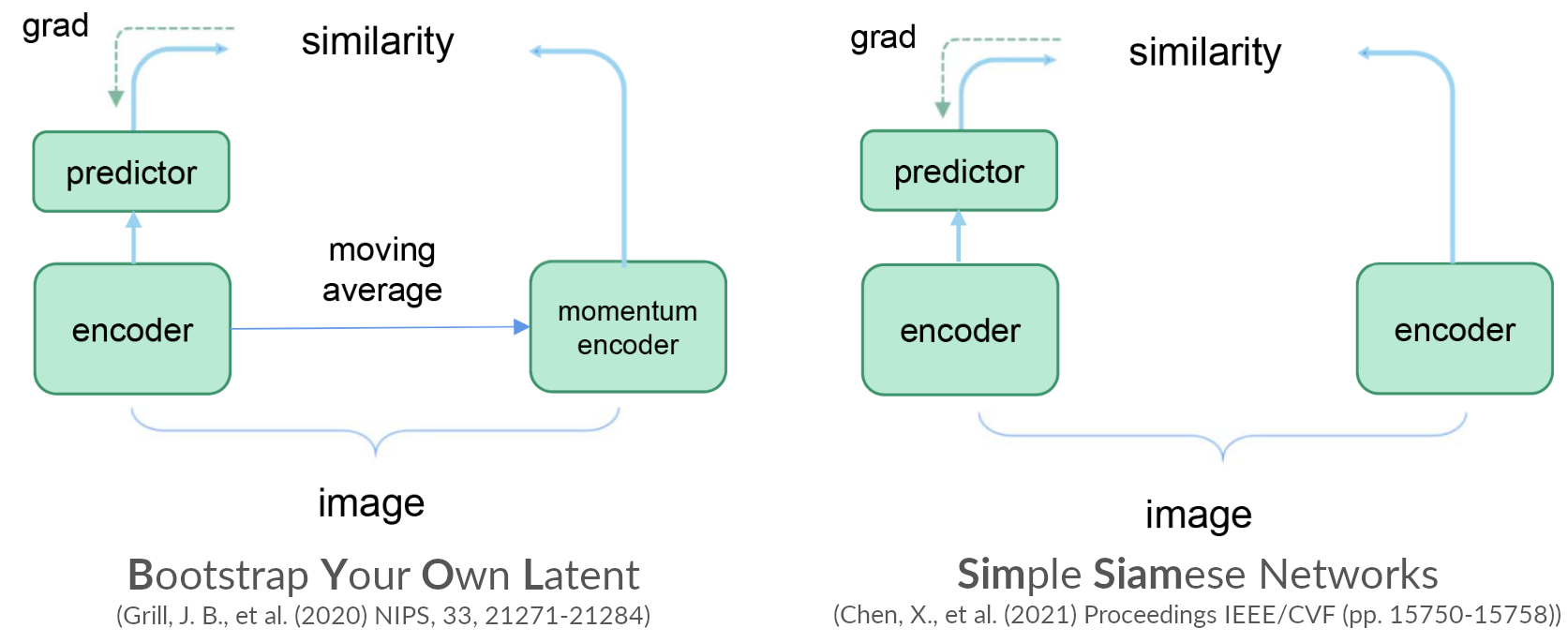
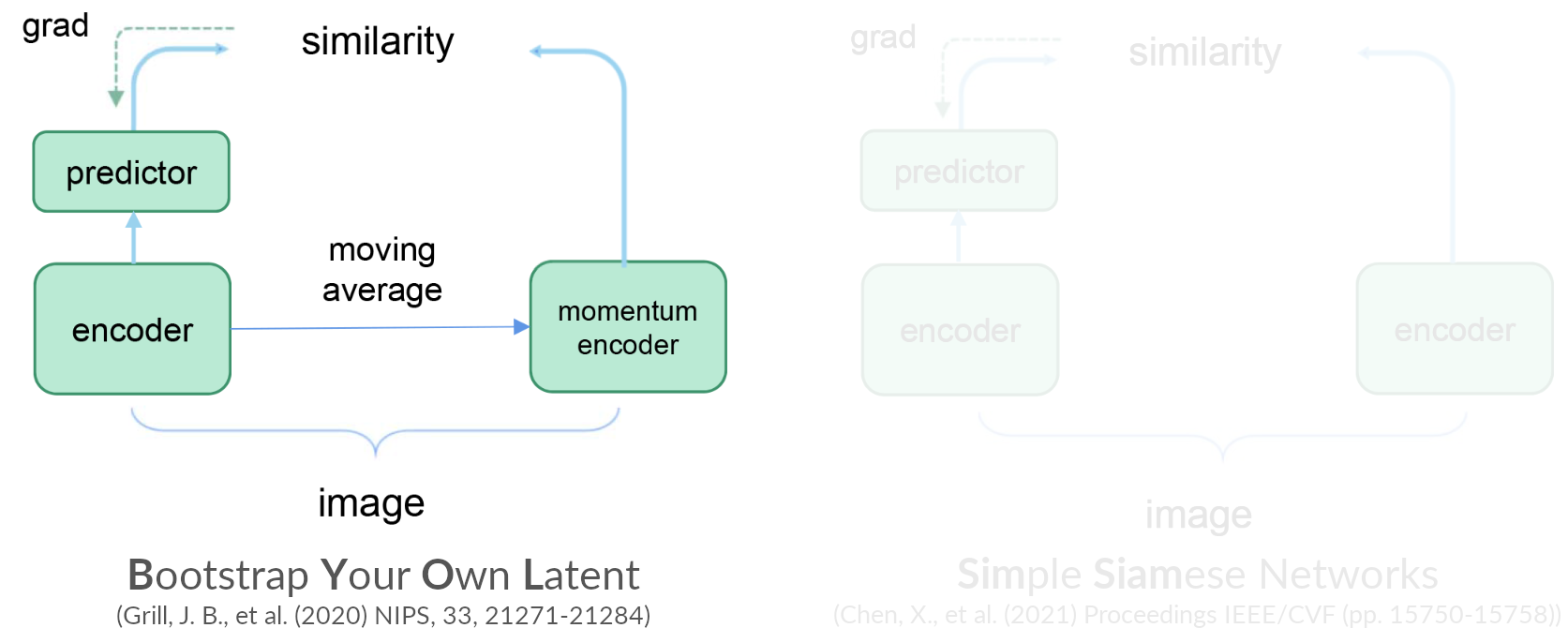
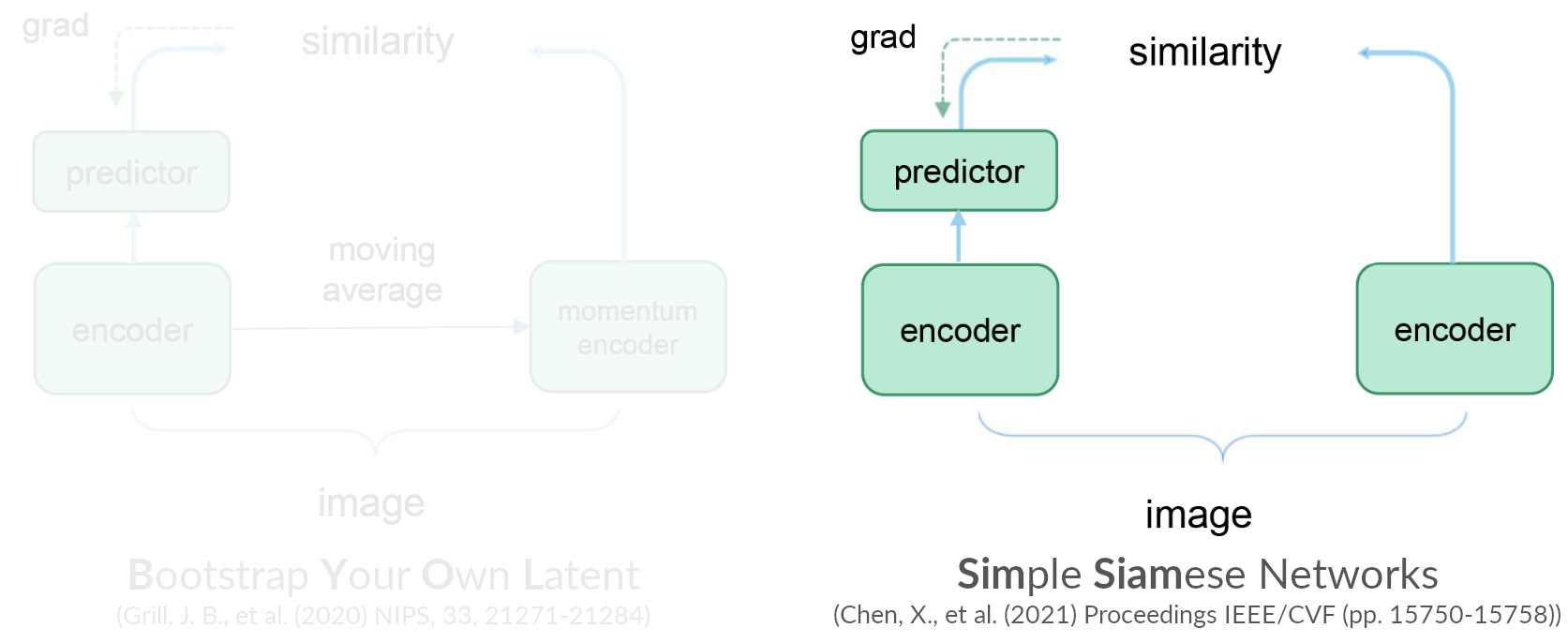
Pretext tasks

Contrastive learning


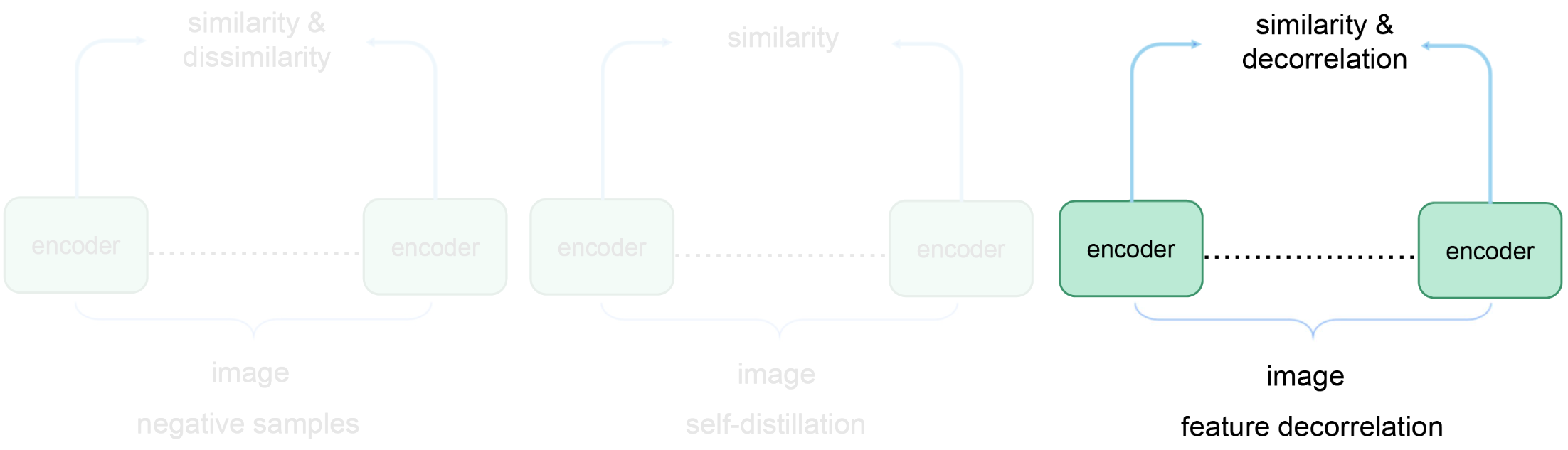
Pretext tasks

Contrastive learning: Feature decorrelation-based


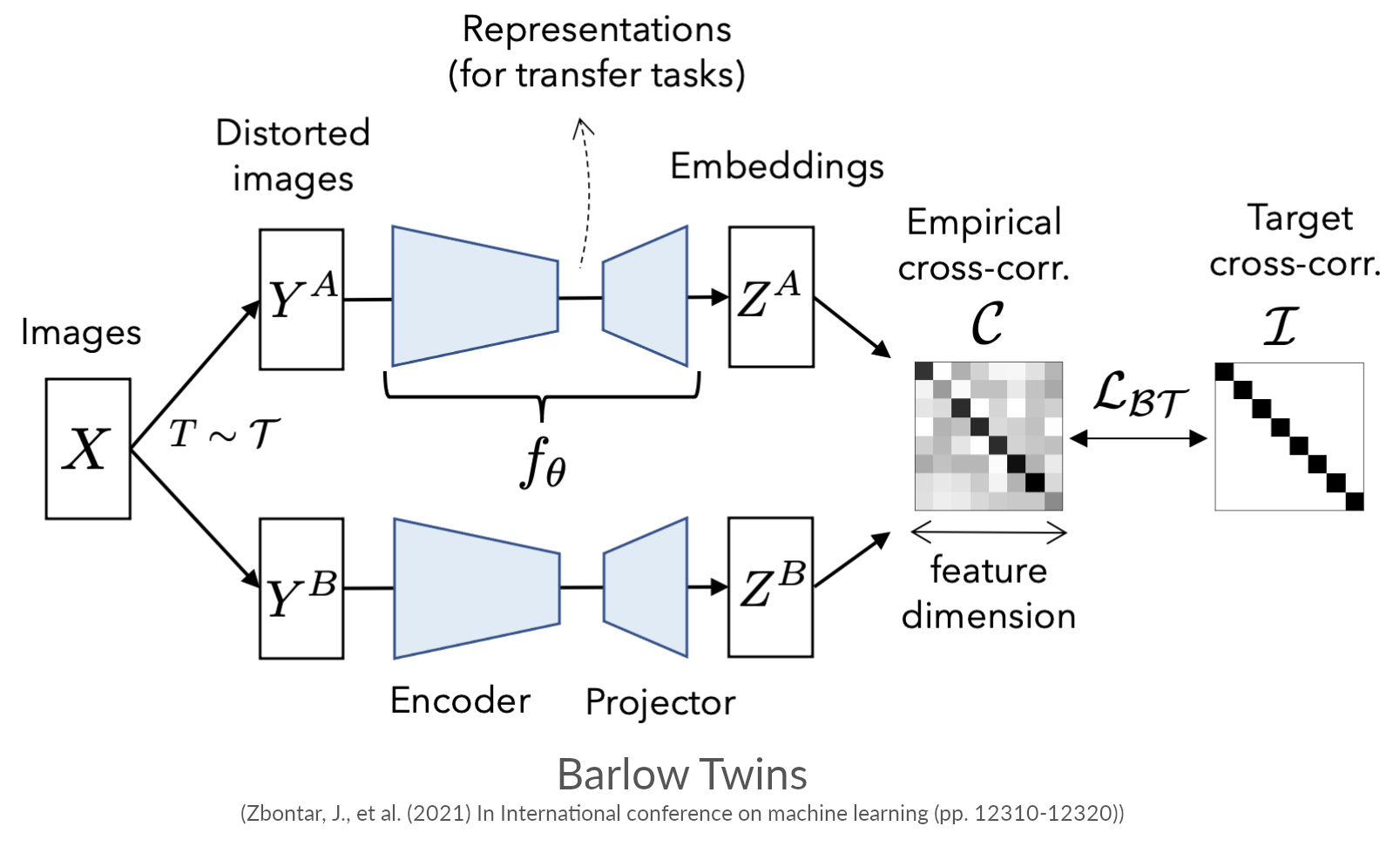
Pretext tasks

Masked modeling


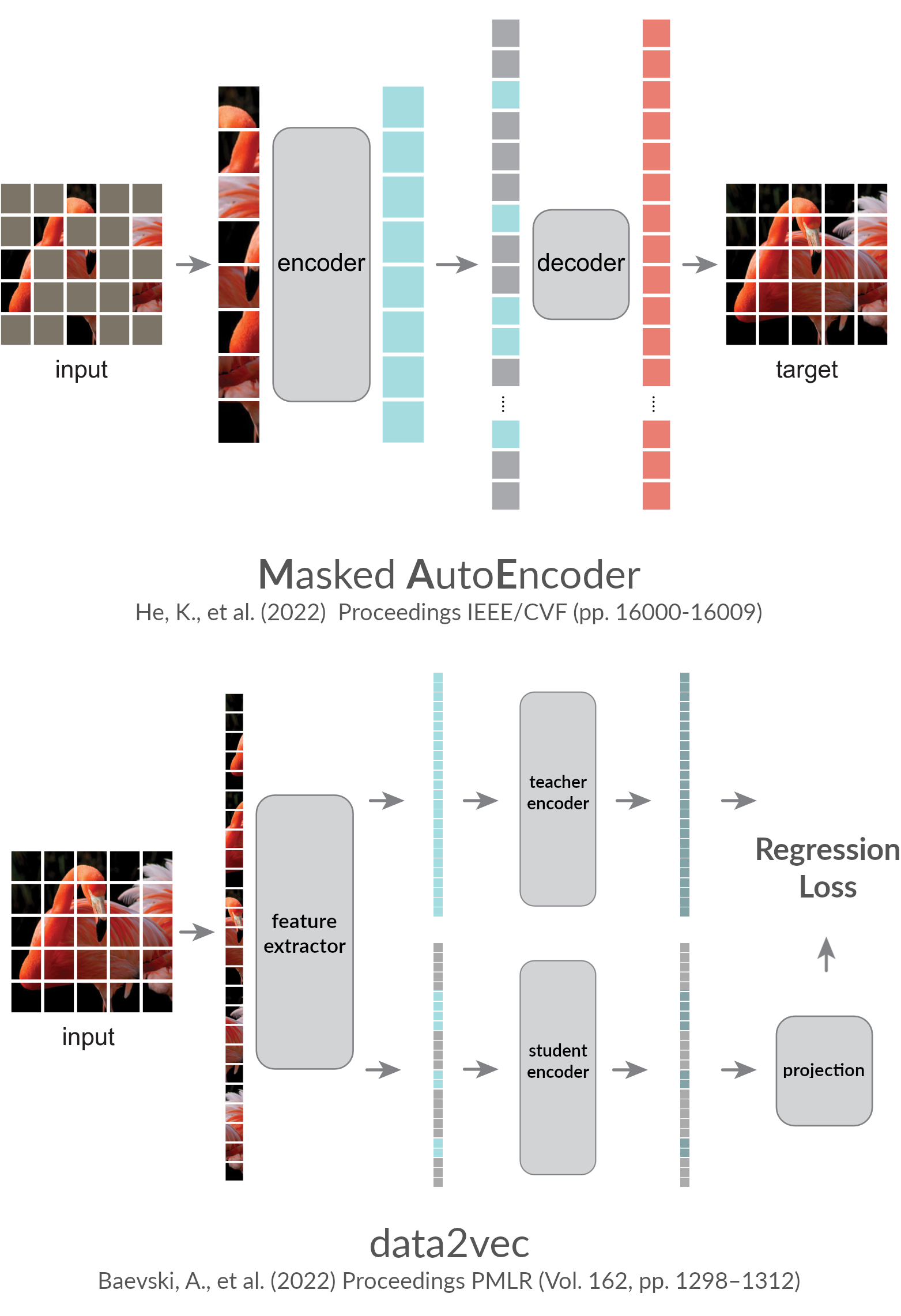
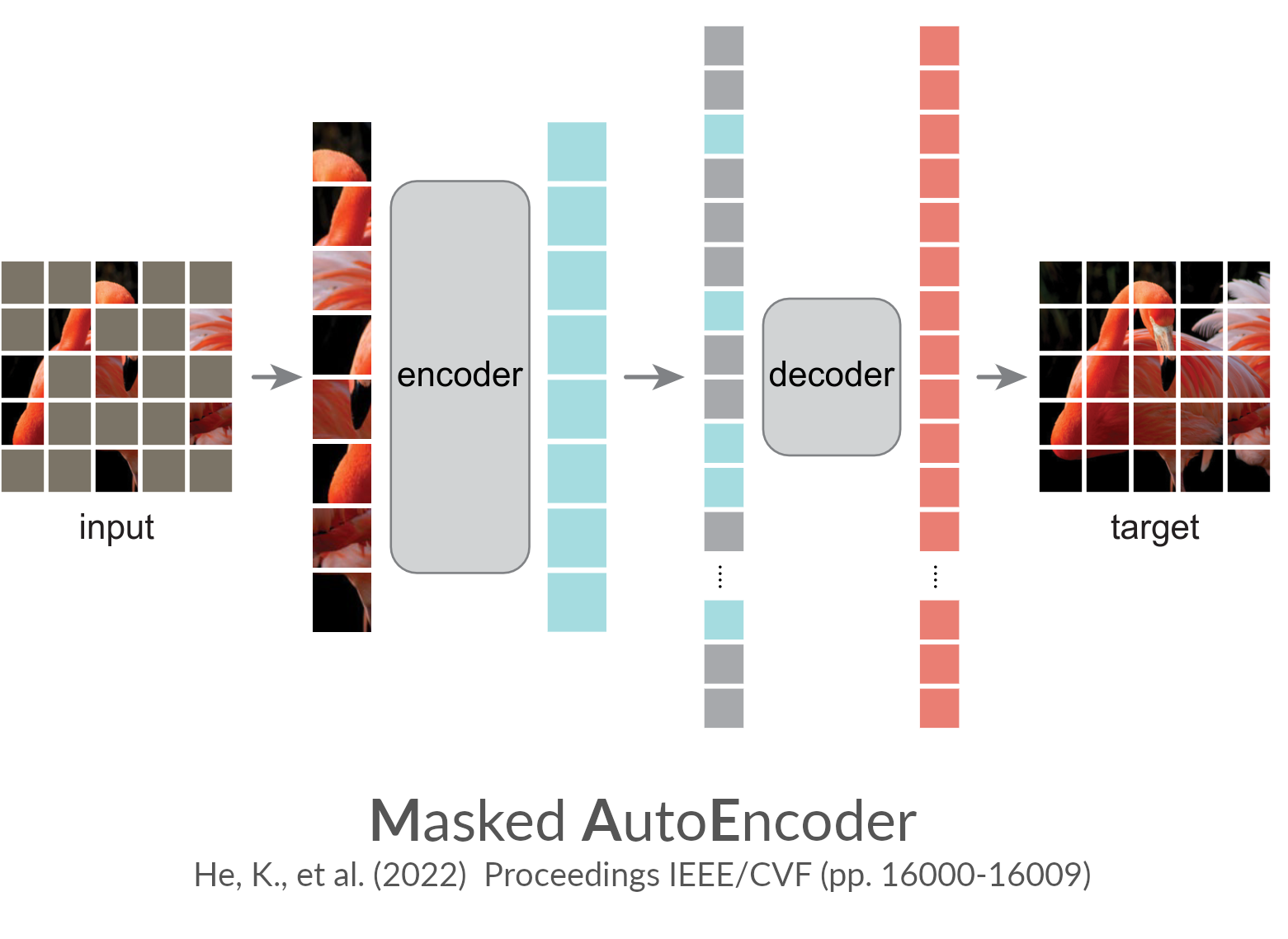
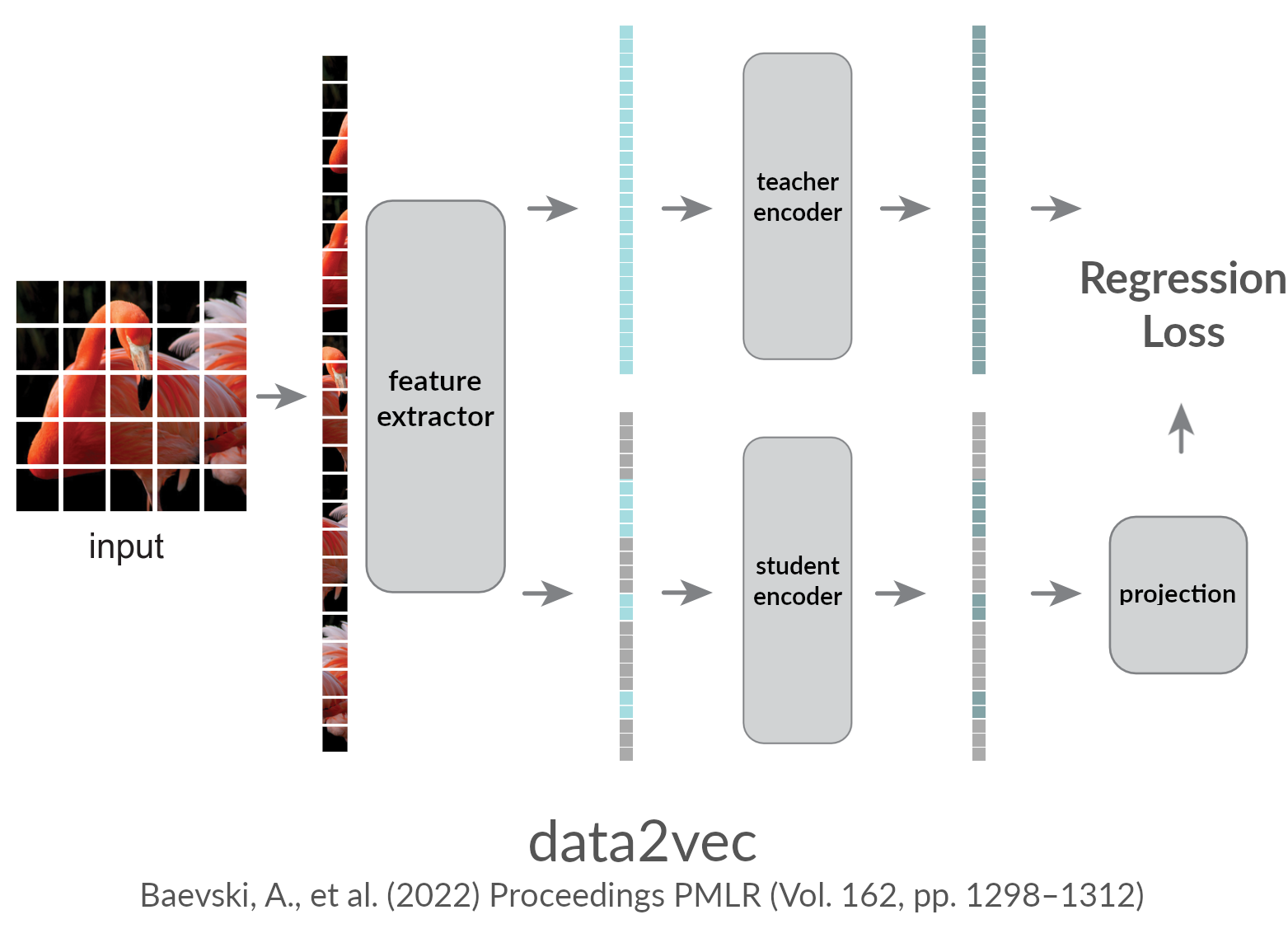
Self-supervised learning

Overview/Applicability to bioacoustics

Overview

What to chose when?



 CLR MM
Dataset size: Data hungry Can handle smaller datasets
Learning: Focus on global views Focus on local views
Scaling: Scale with larger datasets Inferior data scaling
Disadvantages: Vulnerable to overfitting Data-filling challenges

Applicability to bioacoustics

Bioacoustics lives in two domains


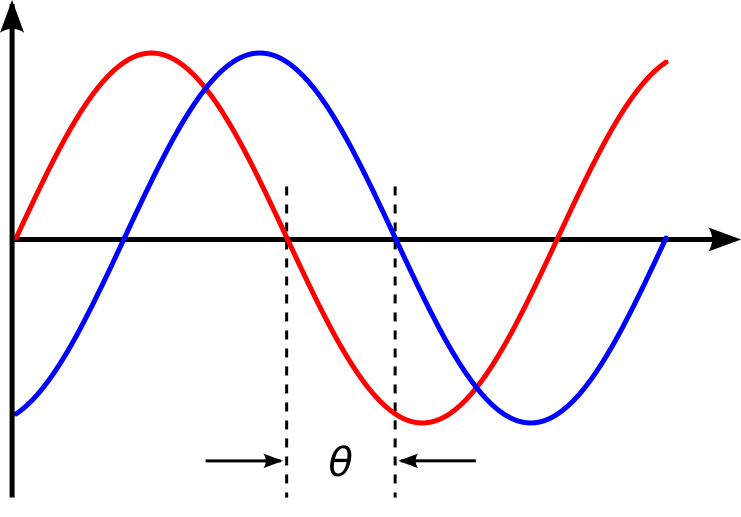
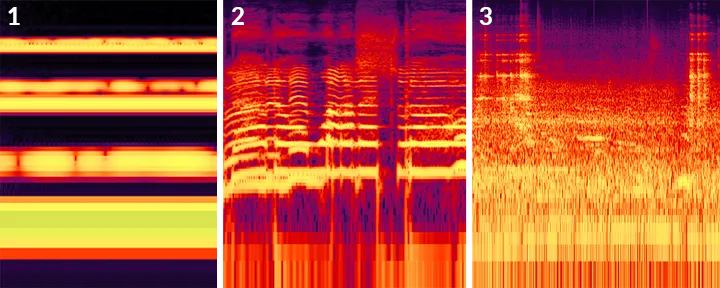
Sound is a temporal phenomenon based on wave-mechanics.
Information is encoded in the time- and phase-domain

  1. Two similar tones cause uneven phase cancellations across frequencies
  2. Two simultaneous voices with similar pitch are difficult to tell apart
  3. Noisy and complex auditory scenes make it particularly difficult to distinguish sound events

Often-used log scaling biases the input towards human hearing

Computer vision models are empirically a good fit, but conceptually they're not

Applicability to bioacoustics

Variable sample-rates


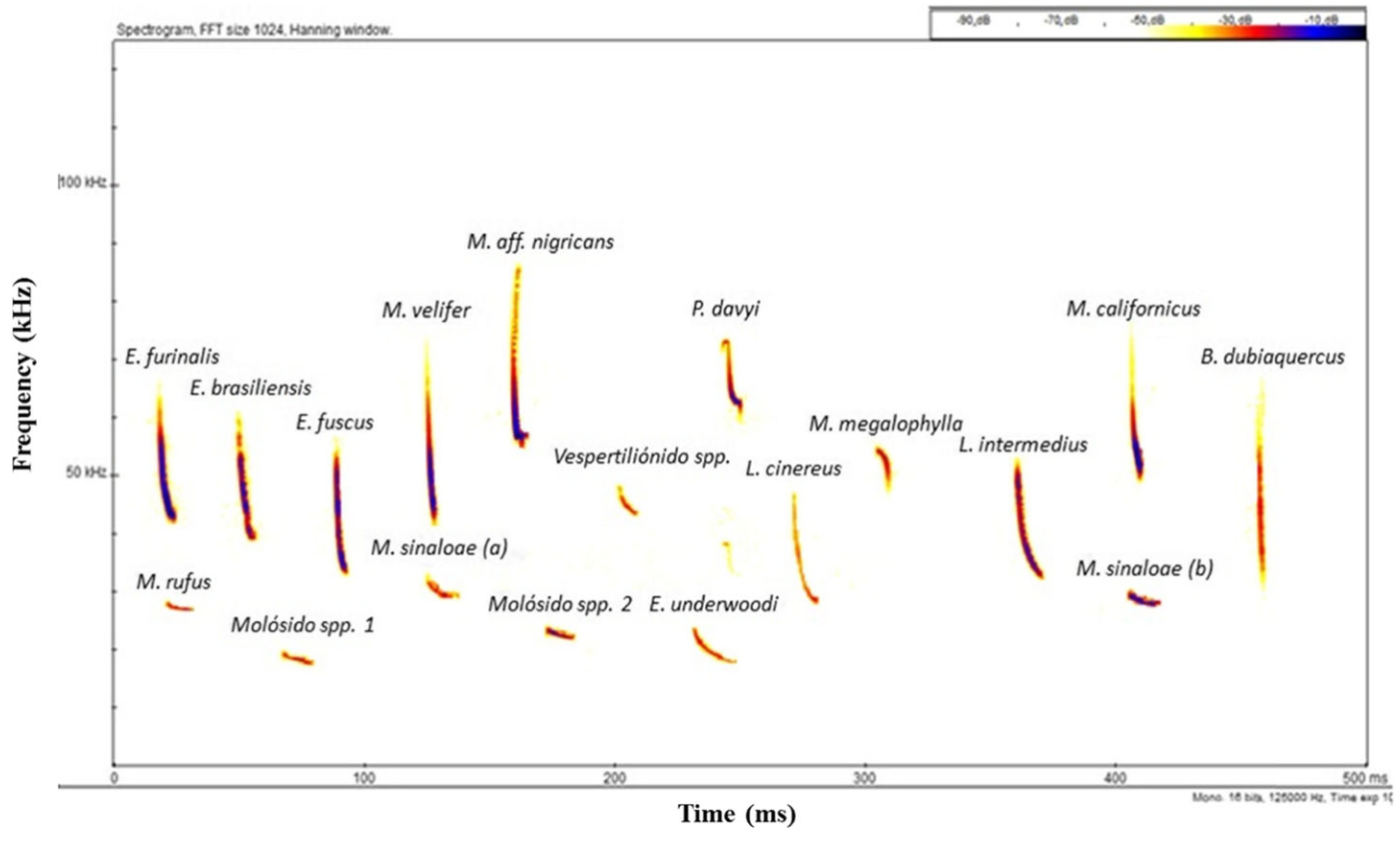
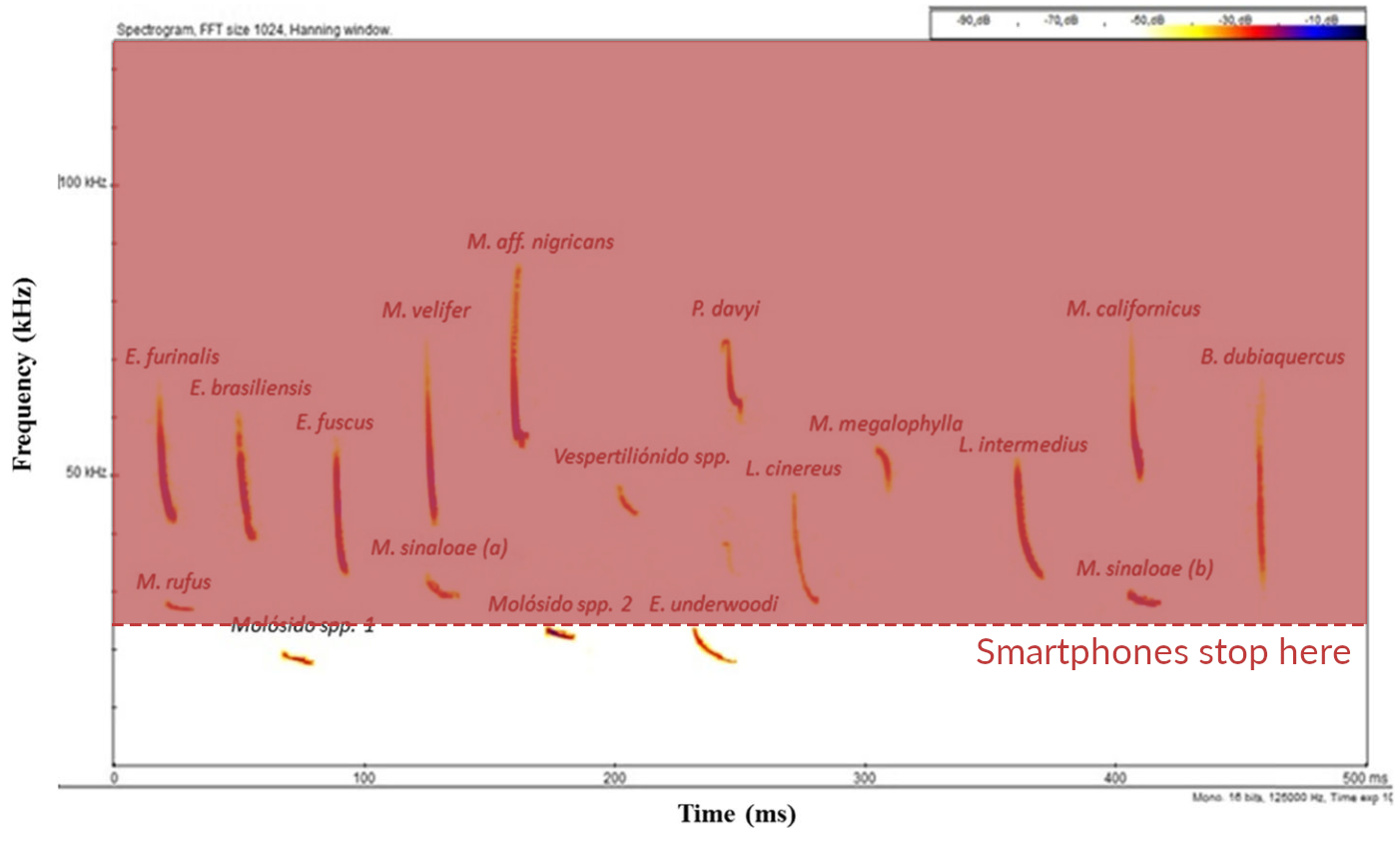
Bioacoustic occurs over a very wide frequency range

Rodríguez-Aguilar, G., et al. (2017) Urban Ecosystems, 20(2), 477–488

Applicability to bioacoustics

Data sparsity


Animal vocalizations are short and rare events

  • For example:
    • MeerKAT [1]: 184h of labeled audio, of which 7.8h (4.2%) contain meerkat vocalizations
    • BirdVox-full-night [2]: 4.5M clips, each of duration 150 ms, only 35k (0.7%) are positive
    • Hainan gibbon calls [3]: 256h of fully labeled PAM data with 1246 few-seconds events (0.01%)
  • Marine datasets have even higher reported sparsity levels [4]

[1] Schäfer-Zimmermann, J. C., et al. (2024). Preprint at arXiv:2406.01253

[2] Lostanlen, V., et al. (2018) IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)

[3] Dufourq, E., et al. (2021) Remote Sensing in Ecology and Conservation, 7(3), 475-487.

[4] Allen, A. N., et al. (2021) Frontiers in Marine Science, 8, 607321

Applicability to bioacoustics

Our response (not necessarily the best) to these challenges



    animal2vec

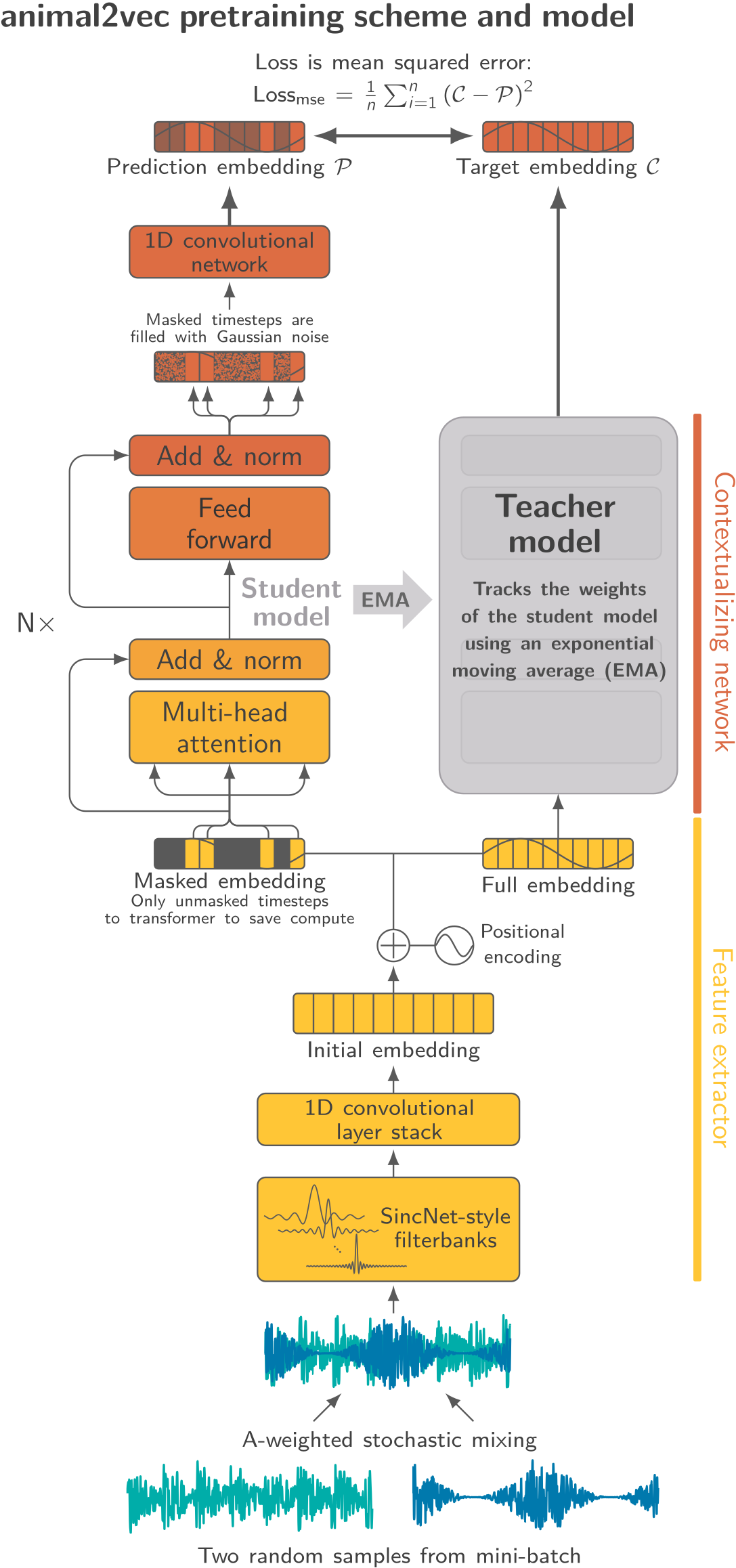
  • Masked-based self-distillation using raw audio input
    • Better with sparse data as no negative-mining is done
    • Makes use of the phase information as we are not calculating spectrograms

Schäfer-Zimmermann, J. C., et al. (2024). Preprint at arXiv:2406.01253

Let's take a break

Next: Transformer

The original transformer

A now widely used domain-agnostic neural network architecture


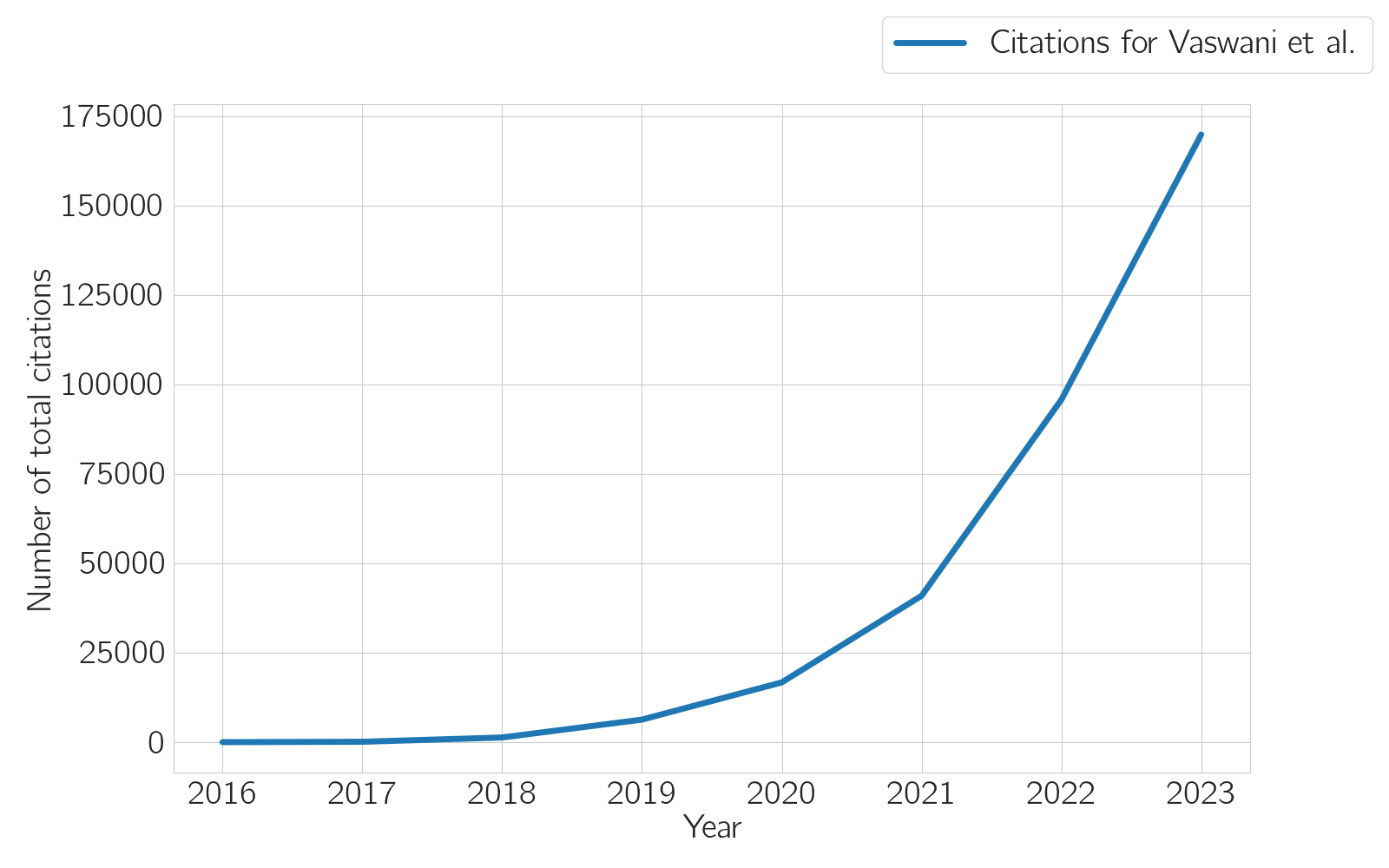
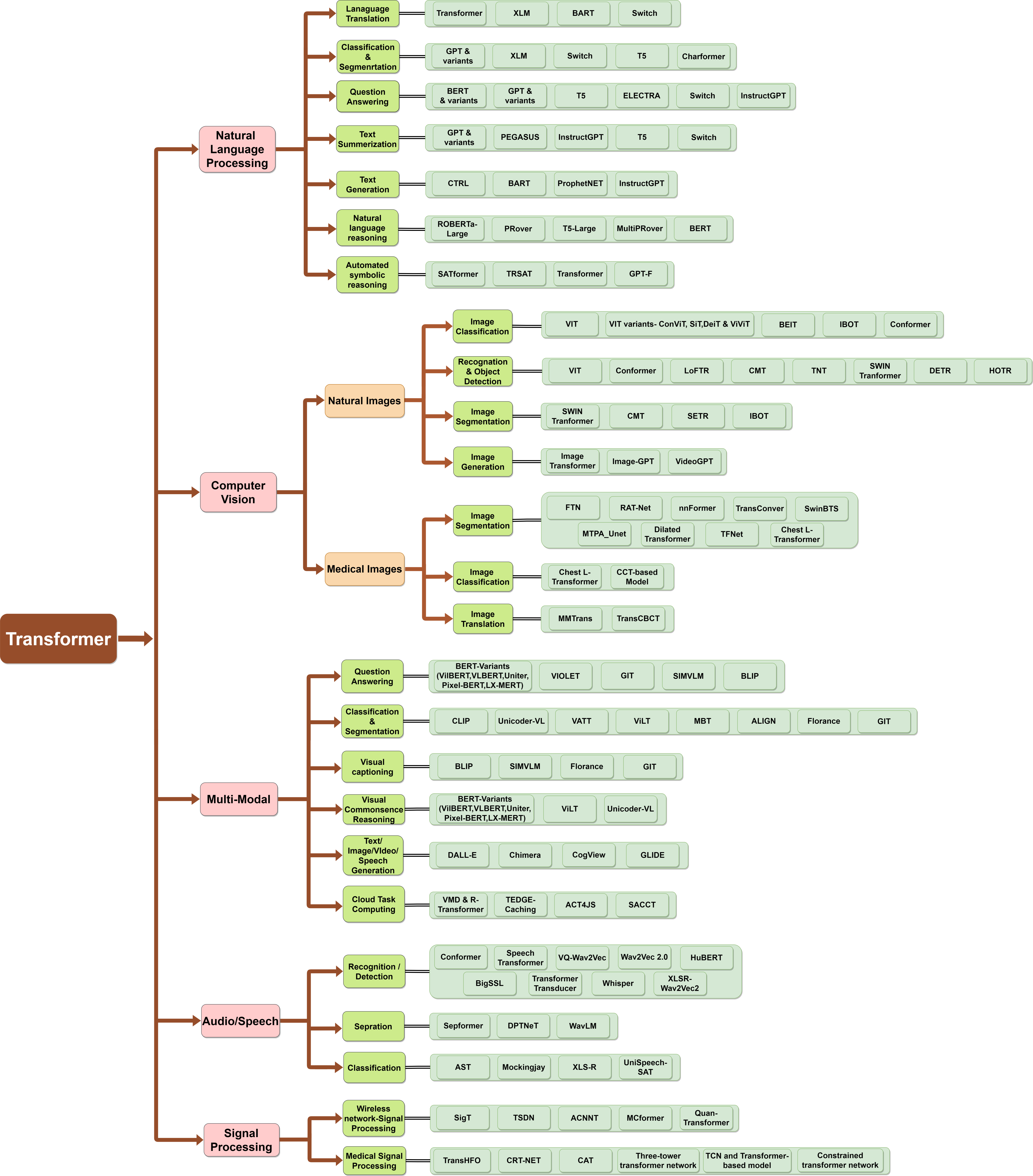
Islam, S., et al. (2024) Expert Systems with Applications, 241, 122666

The original transformer




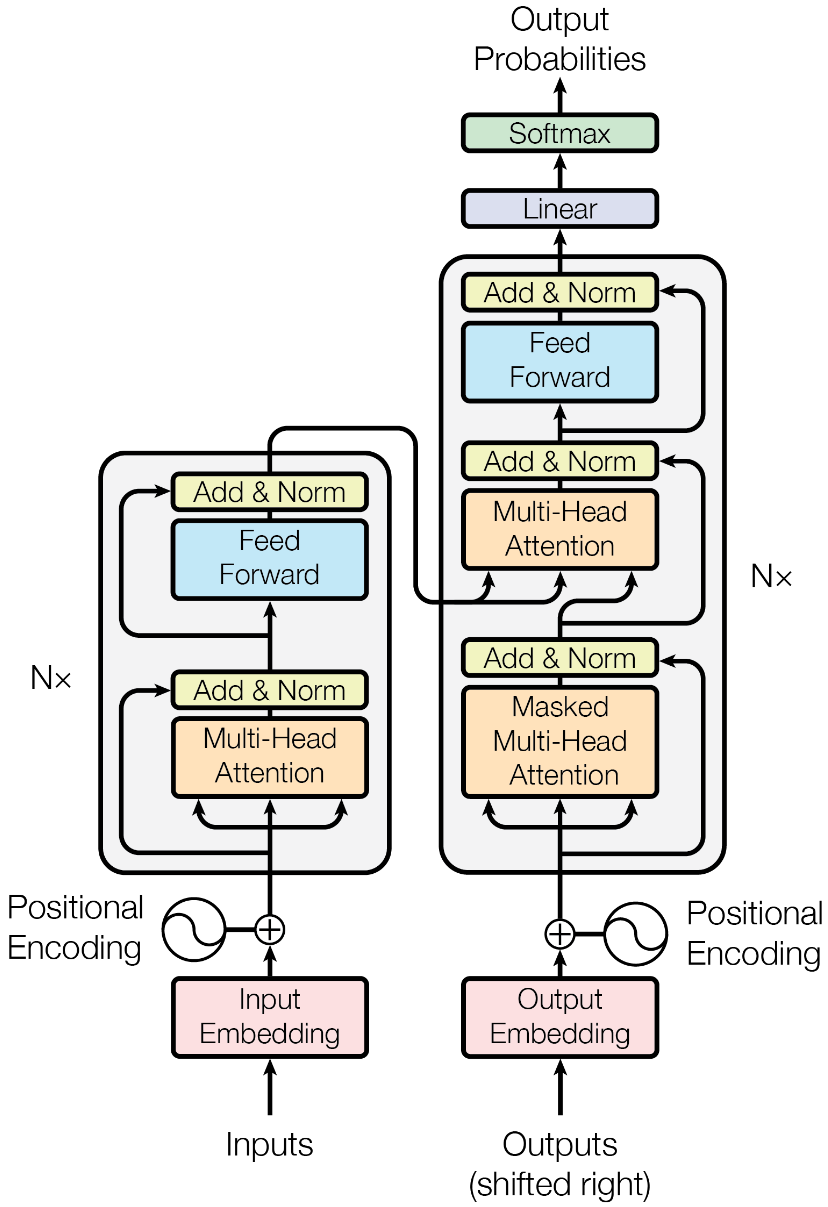
Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



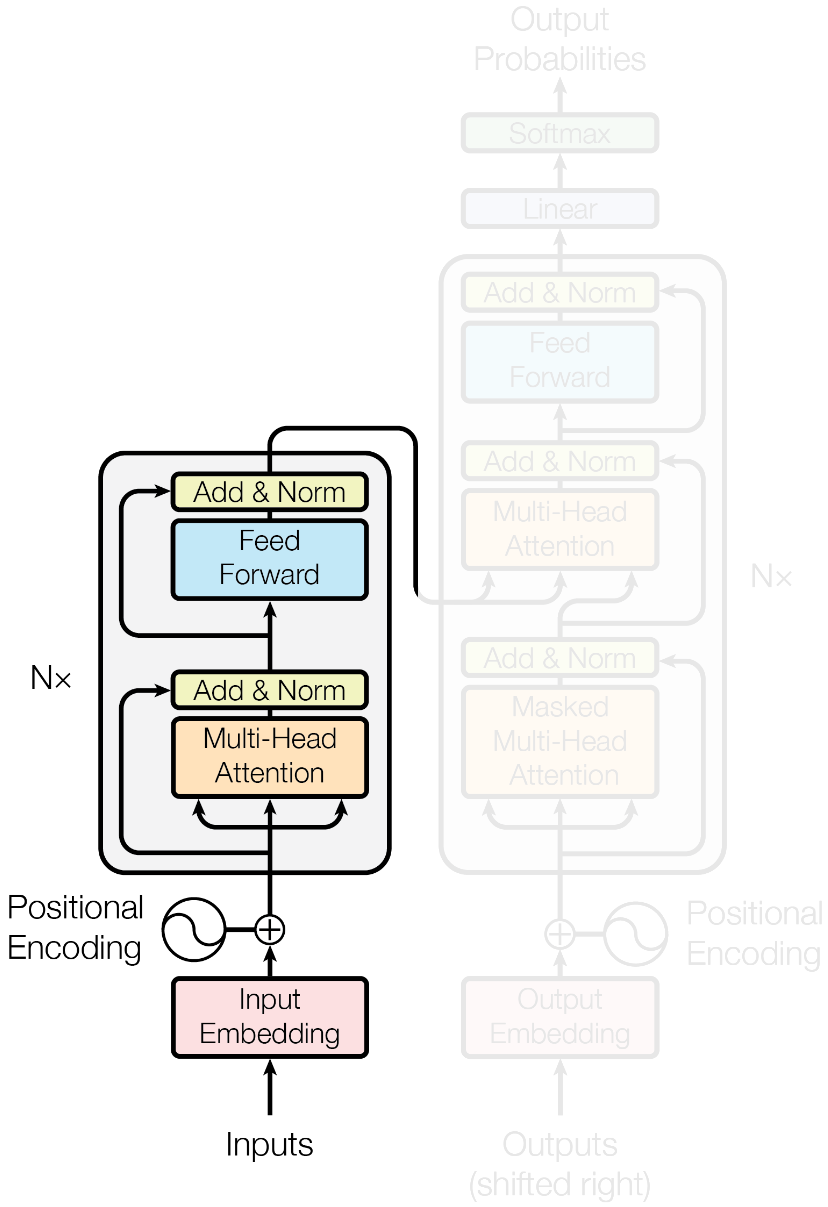
  • An encoding component


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



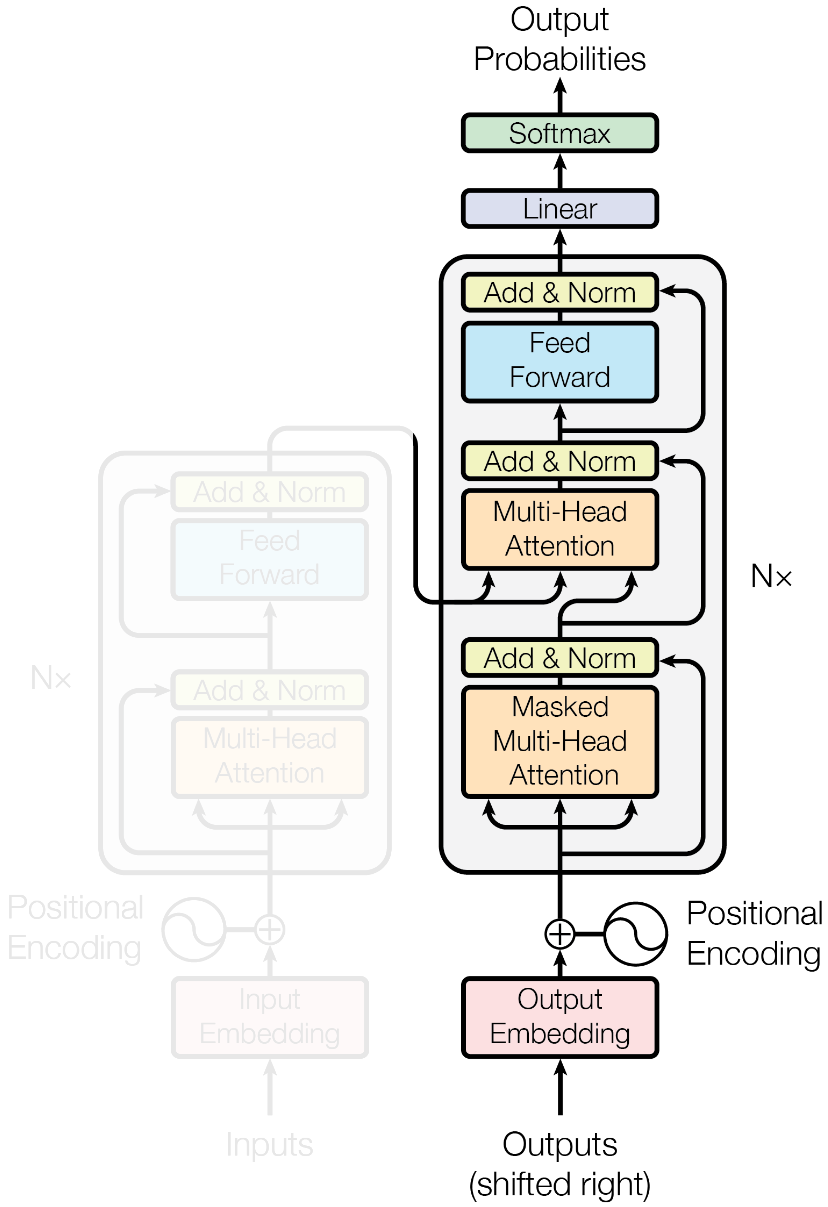
  • An encoding component
  • A decoding component


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



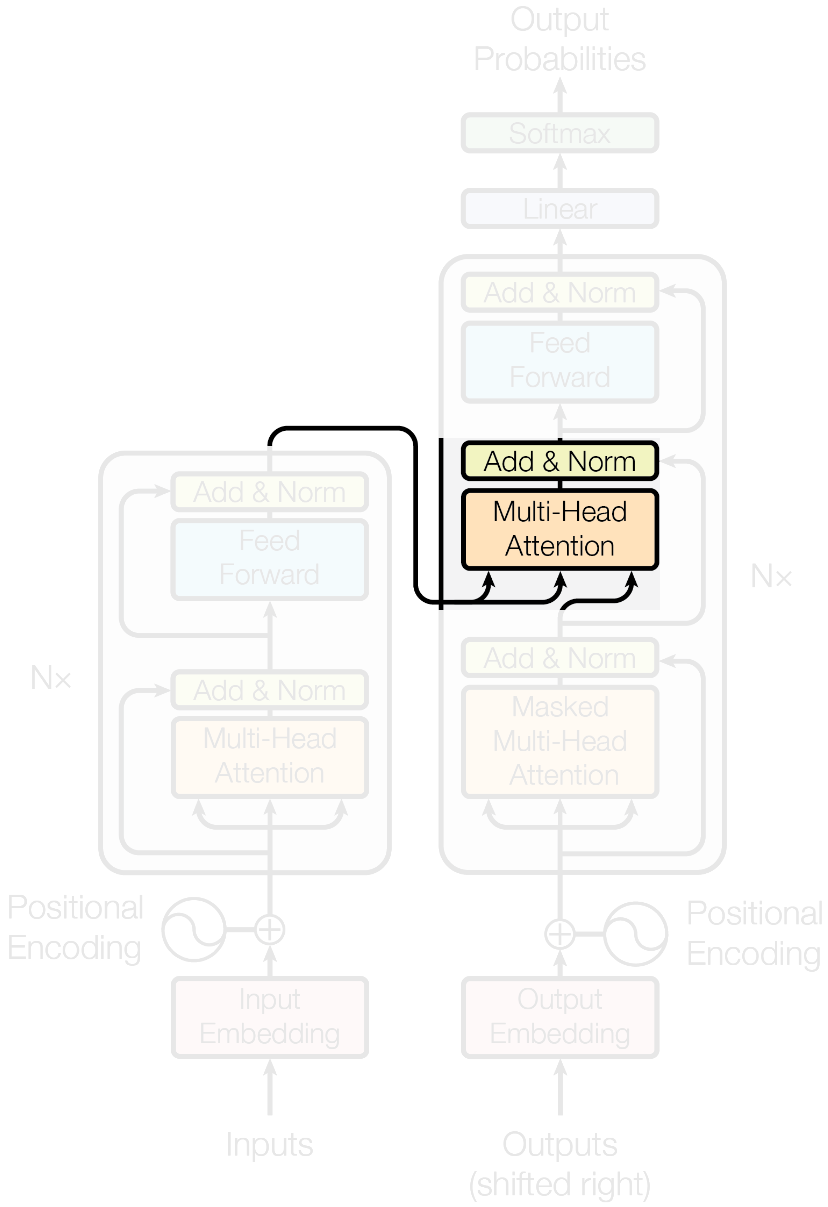
  • An encoding component
  • A decoding component
  • Connections between them


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



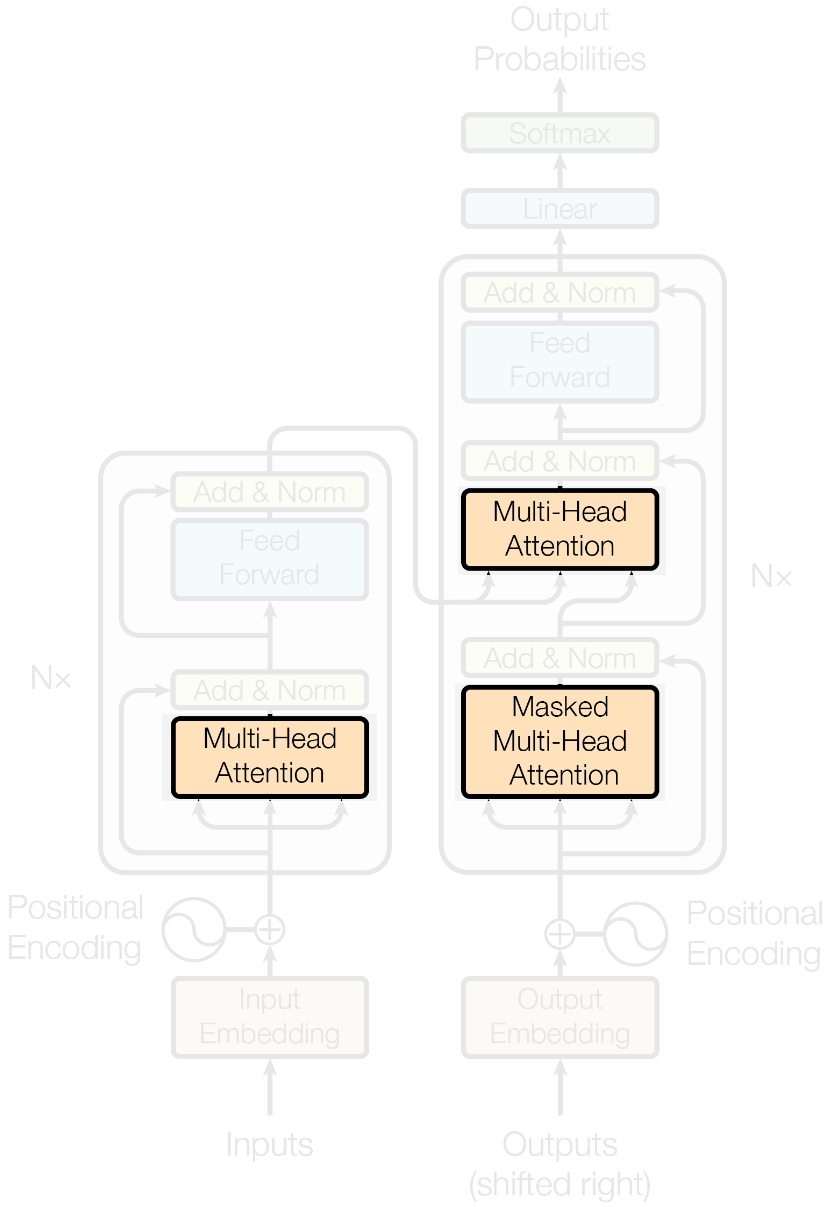
  • An encoding component
  • A decoding component
  • Connections between them
  • The attention mechanism


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



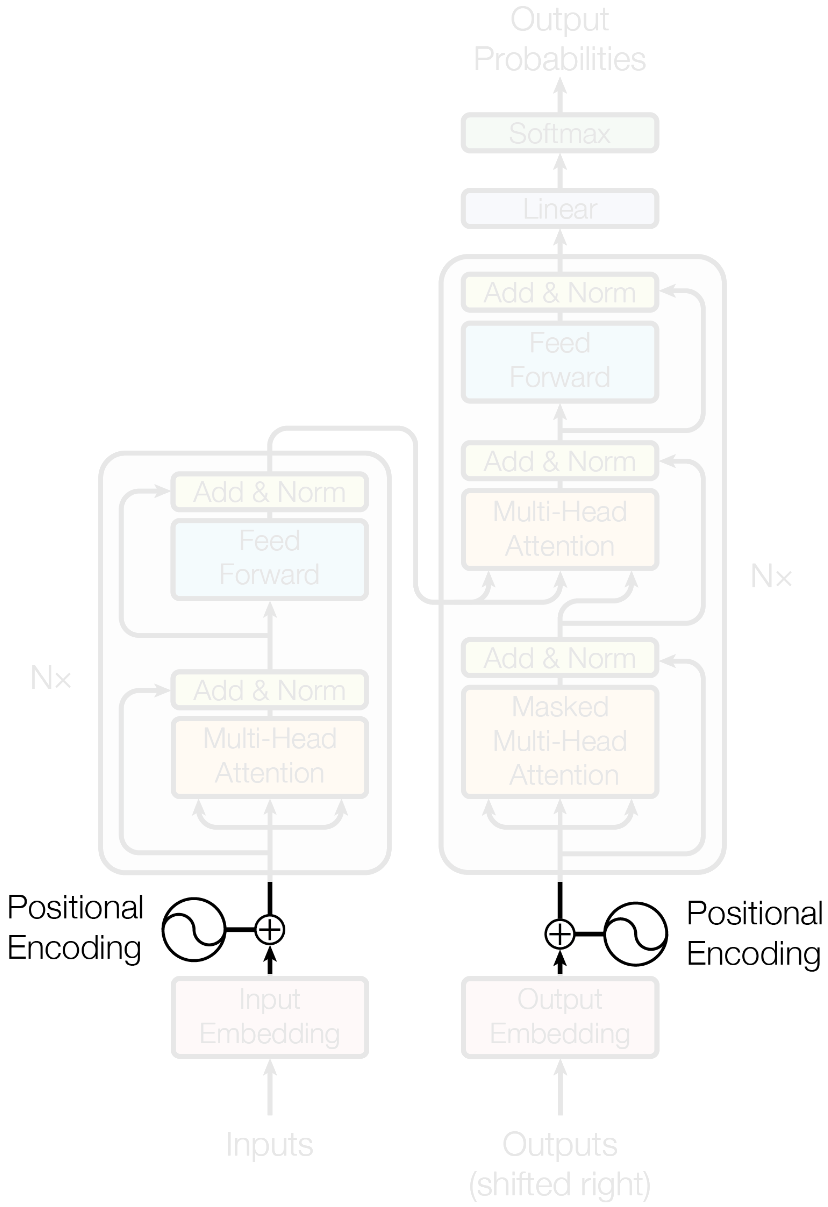
  • An encoding component
  • A decoding component
  • Connections between them
  • The attention mechanism
  • A positional encoding


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The original transformer



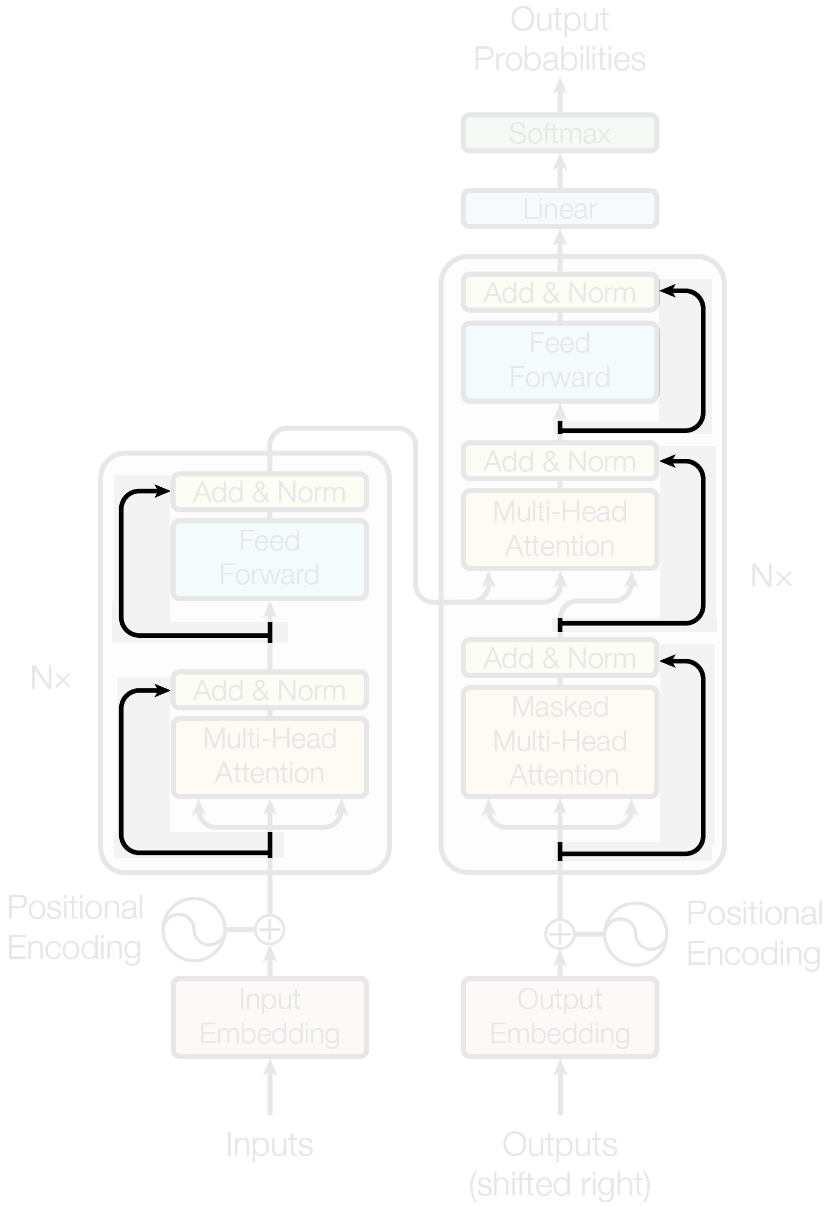
  • An encoding component
  • A decoding component
  • Connections between them
  • The attention mechanism
  • A positional encoding
  • Residual connections


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

The encoder decoder structure


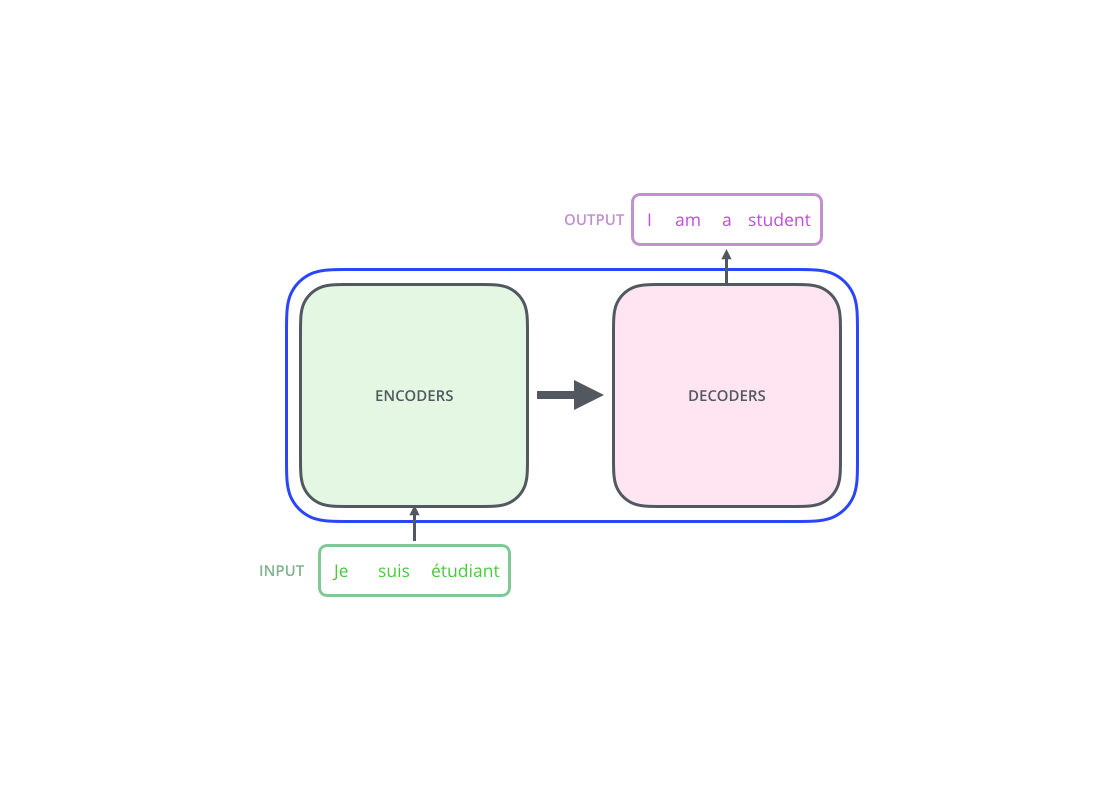
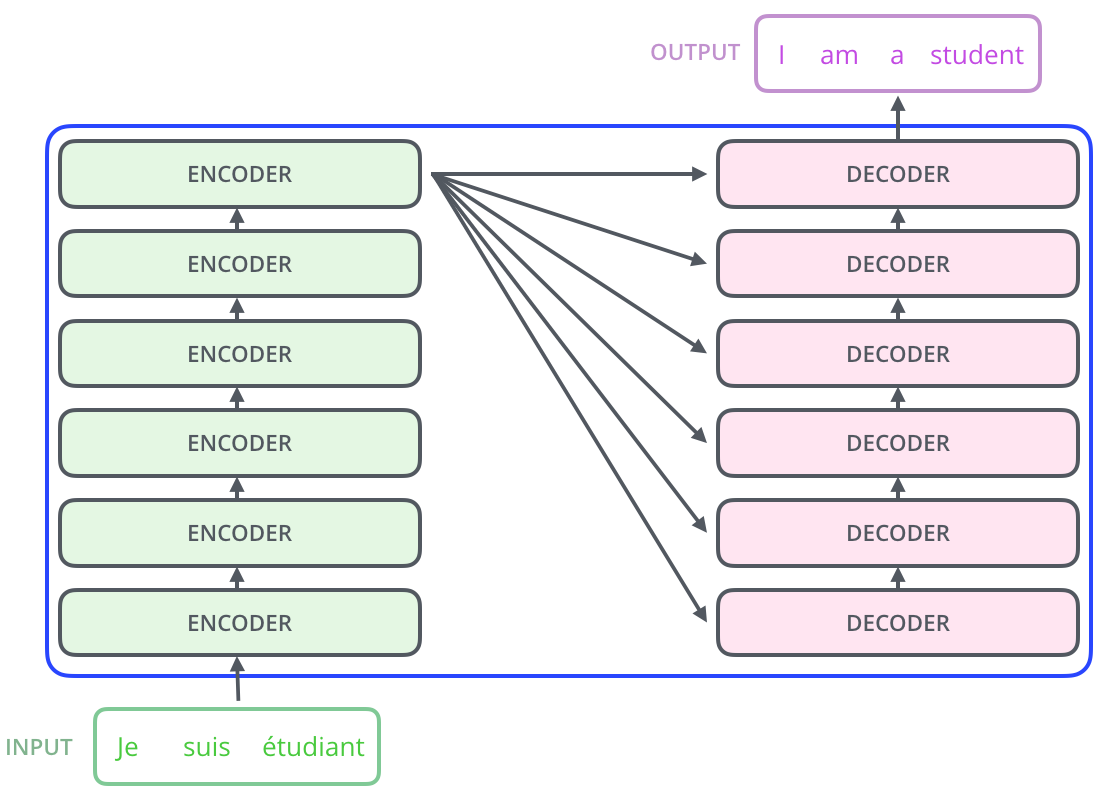
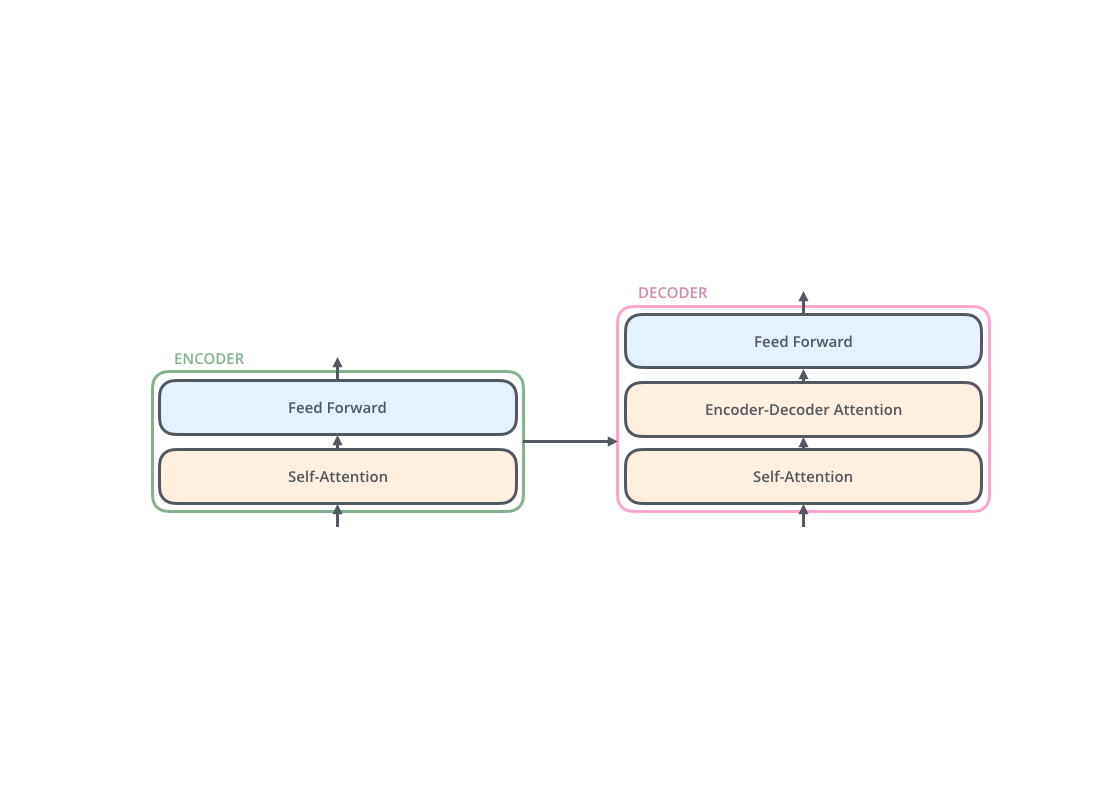
Jay Alammar - The Illustrated Transformer

Attention mechanism


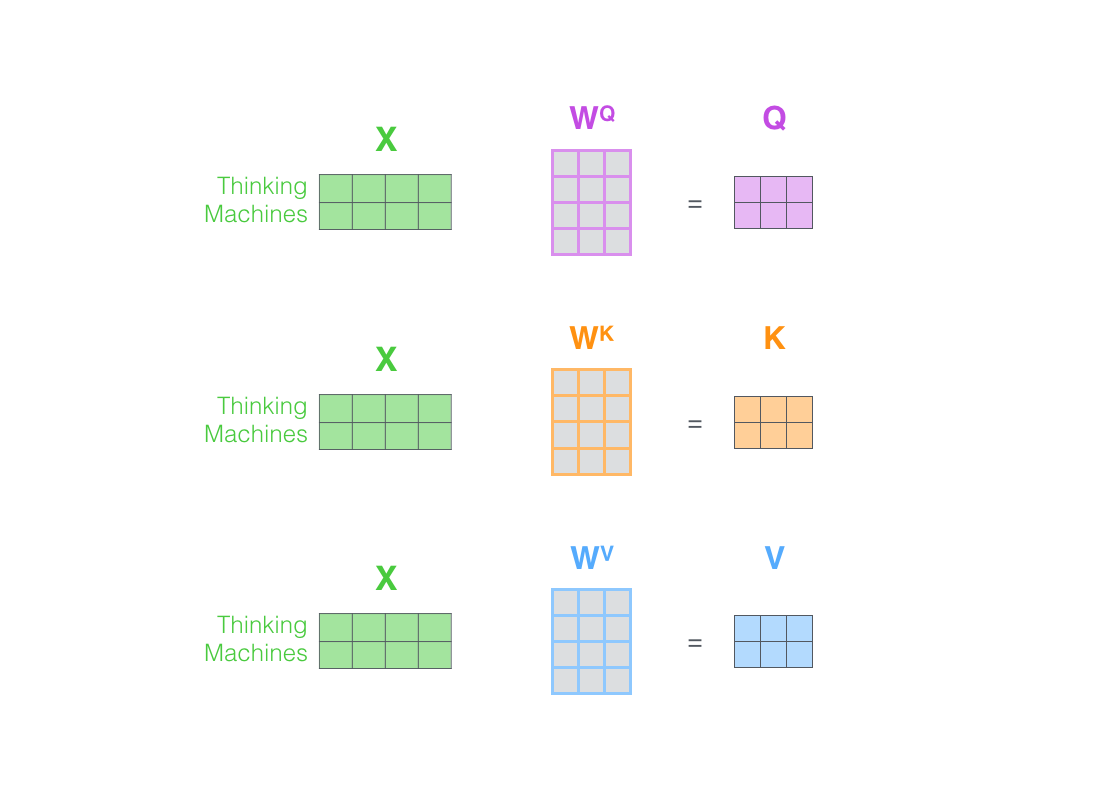
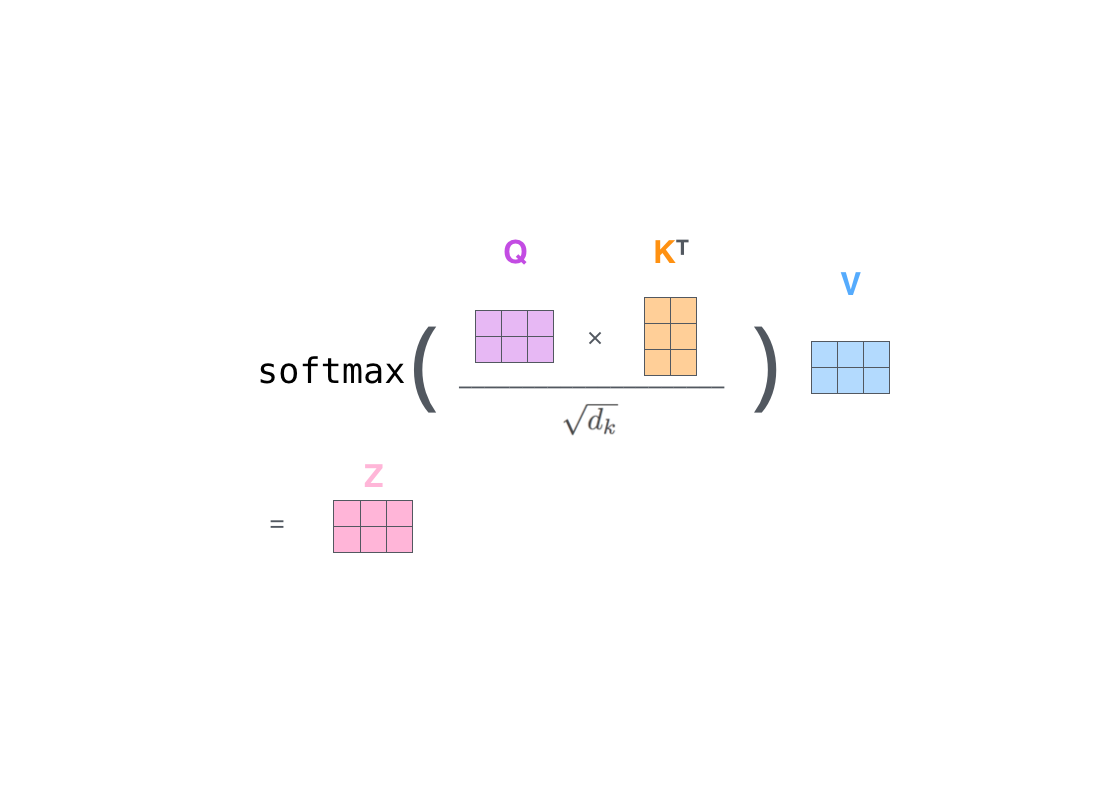
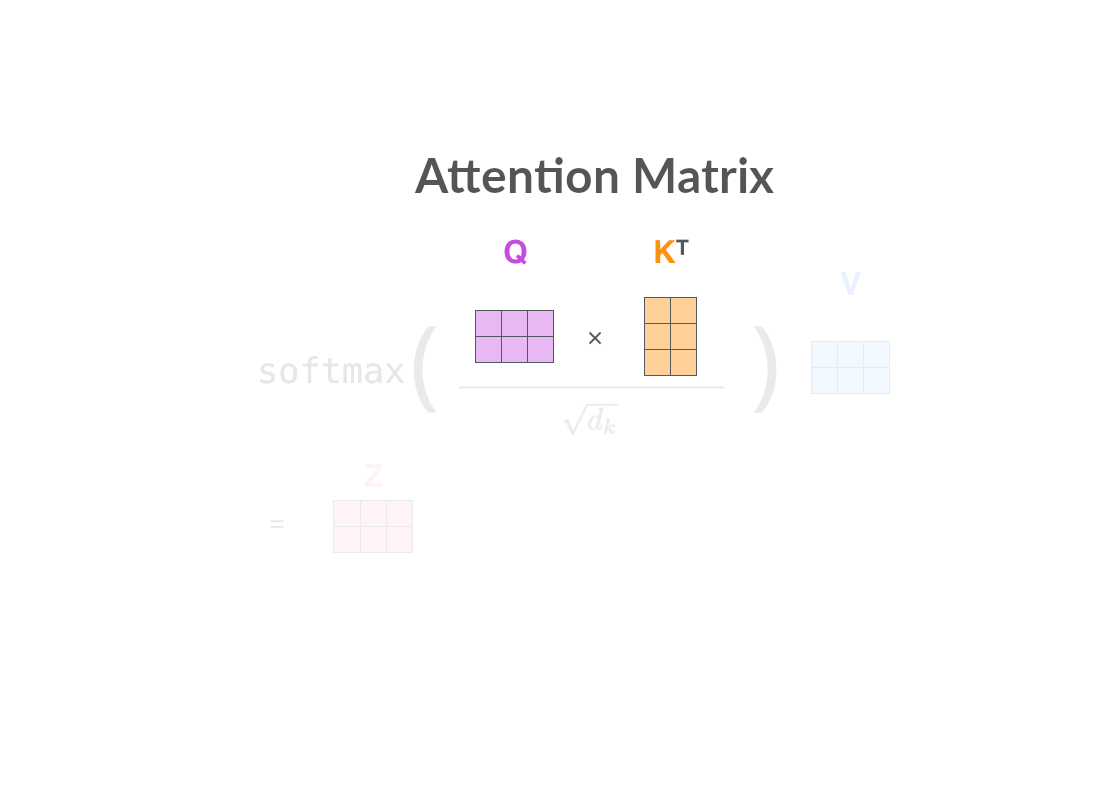
Jay Alammar - The Illustrated Transformer

Attention matrix


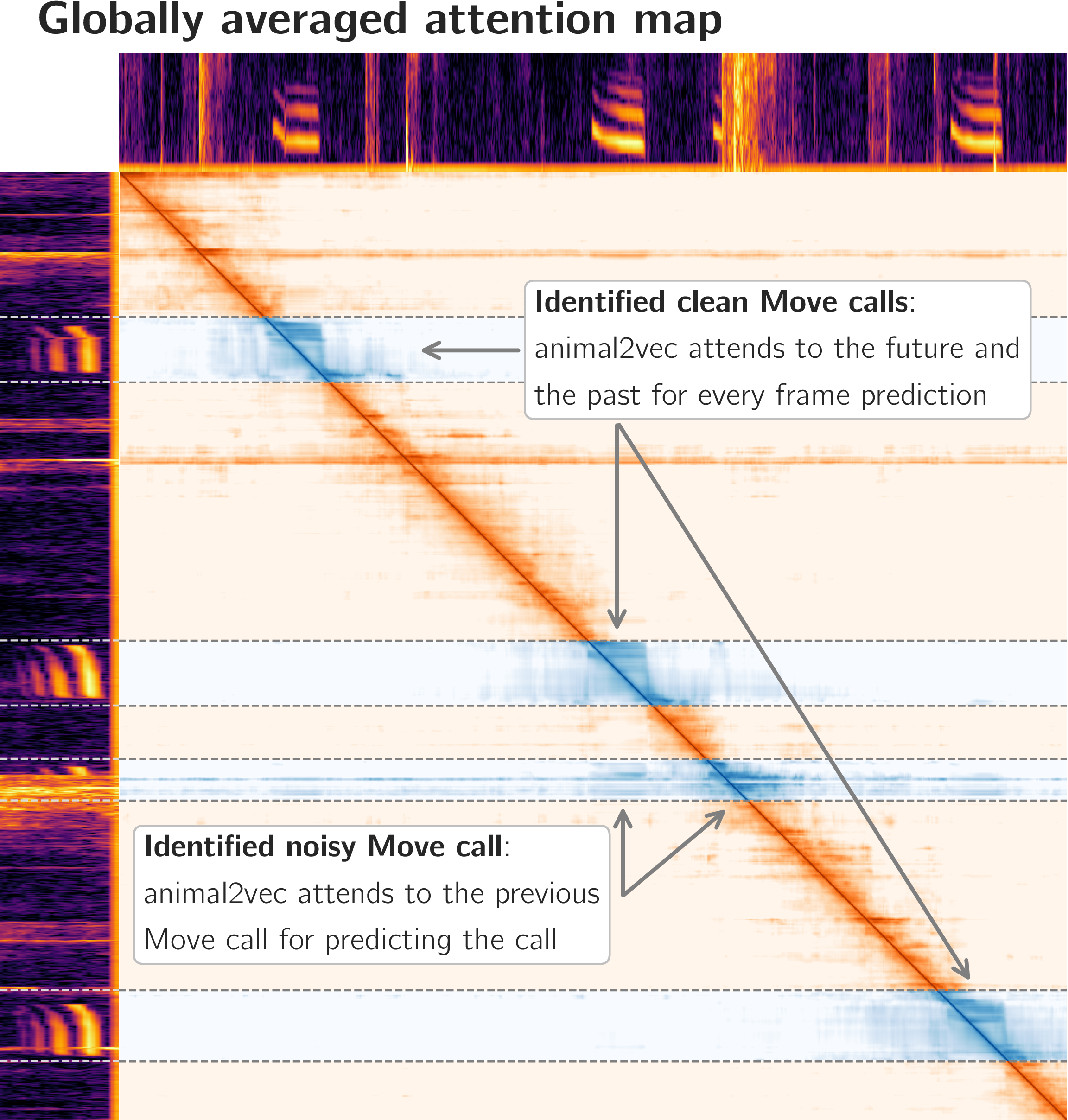
Schäfer-Zimmermann, J. C., et al. (2024). Preprint at arXiv:2406.01253

Attention matrix


\[\text{"Thinking": } \begin{pmatrix} a_{1} & a_{2} \end{pmatrix} \] \[\text{"Machines": } \begin{pmatrix} b_{1} & b_{2} \end{pmatrix} \]

\[\text{Input: } X=\begin{pmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{pmatrix} \]

Attention matrix


\[\text{Query Matrix: } Q= \begin{pmatrix} a_{1} & a_{2}\\ b_{1} & b_{2} \end{pmatrix} \cdot \begin{pmatrix} W^{q}_{1} & W^{q}_{2}\\ W^{q}_{3} & W^{q}_{4}\\ \end{pmatrix} \] \[ = \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{4} + b_{2}W^{q}_{4} \end{pmatrix} \]

Attention matrix


\[\text{Query Matrix: } Q= \begin{pmatrix} a_{1} & a_{2}\\ b_{1} & b_{2} \end{pmatrix} \cdot \begin{pmatrix} W^{q}_{1} & W^{q}_{2}\\ W^{q}_{3} & W^{q}_{4}\\ \end{pmatrix} \] \[ = \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{4} + b_{2}W^{q}_{4} \end{pmatrix} \]

\[\text{Key Matrix: } K= \begin{pmatrix} a_{1} & a_{2}\\ b_{1} & b_{2} \end{pmatrix} \cdot \begin{pmatrix} W^{k}_{1} & W^{k}_{2}\\ W^{k}_{3} & W^{k}_{4}\\ \end{pmatrix} \] \[ = \begin{pmatrix} a_{1}W^{k}_{1} + a_{2}W^{k}_{3} & a_{1}W^{k}_{2} + a_{2}W^{k}_{4} \\ b_{1}W^{k}_{1} + b_{2}W^{k}_{3} & b_{1}W^{k}_{2} + b_{2}W^{k}_{4} \end{pmatrix} \]

Attention matrix


\[\text{Attention Matrix: } Q \cdot K^{T}=\] \[ \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{2} + b_{2}W^{q}_{4} \end{pmatrix} \cdot \begin{pmatrix} a_{1}W^{k}_{1} + a_{2}W^{k}_{3} & b_{1}W^{k}_{1} + b_{2}W^{k}_{3} \\ a_{1}W^{k}_{2} + a_{2}W^{k}_{4} & b_{1}W^{k}_{2} + b_{2}W^{k}_{4} \end{pmatrix} \]

\[ = \begin{pmatrix} (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3}) + (a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \\ (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(b_{1}W^{q}_{2} + b_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3})+(b_{1}W^{q}_{2} + b_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \end{pmatrix} \]

Attention matrix


\[\text{Attention Matrix: } Q \cdot K^{T}=\] \[ \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{2} + b_{2}W^{q}_{4} \end{pmatrix} \cdot \begin{pmatrix} a_{1}W^{k}_{1} + a_{2}W^{k}_{3} & b_{1}W^{k}_{1} + b_{2}W^{k}_{3} \\ a_{1}W^{k}_{2} + a_{2}W^{k}_{4} & b_{1}W^{k}_{2} + b_{2}W^{k}_{4} \end{pmatrix} \]

\[ = \begin{pmatrix} ({\bf\color{green} a_{1}}{\bf\color{purple}W^{q}_{1}} + {\bf\color{green} a_{2}}{\bf\color{purple}W^{q}_{3}})({\bf\color{green} a_{1}}{\bf\color{orange}W^{k}_{1}} + {\bf\color{green} a_{2}}{\bf\color{orange}W^{k}_{3}})+({\bf\color{green} a_{1}}{\bf\color{purple}W^{q}_{2}} + {\bf\color{green} a_{2}}{\bf\color{purple}W^{q}_{4}})({\bf\color{green} a_{1}}{\bf\color{orange}W^{k}_{2}} + {\bf\color{green} a_{2}}{\bf\color{orange}W^{k}_{4}}) & (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3}) + (a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \\ (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(b_{1}W^{q}_{2} + b_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3})+(b_{1}W^{q}_{2} + b_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \end{pmatrix} \]

All weights from all weight matrices attend to only the first word

Attention matrix


\[\text{Attention Matrix: } Q \cdot K^{T}=\] \[ \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{2} + b_{2}W^{q}_{4} \end{pmatrix} \cdot \begin{pmatrix} a_{1}W^{k}_{1} + a_{2}W^{k}_{3} & b_{1}W^{k}_{1} + b_{2}W^{k}_{3} \\ a_{1}W^{k}_{2} + a_{2}W^{k}_{4} & b_{1}W^{k}_{2} + b_{2}W^{k}_{4} \end{pmatrix} \]

\[ = \begin{pmatrix} (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3}) + (a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \\ (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(b_{1}W^{q}_{4} + b_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & ({\bf\color{green}b_{1}}{\bf\color{purple}W^{q}_{1}} + {\bf\color{green}b_{2}}{\bf\color{purple}W^{q}_{3}})({\bf\color{green}b_{1}}{\bf\color{orange}W^{k}_{1}} + {\bf\color{green}b_{2}}{\bf\color{orange}W^{k}_{3}})+({\bf\color{green}b_{1}}{\bf\color{purple}W^{q}_{2}} + {\bf\color{green}b_{2}}{\bf\color{purple}W^{q}_{4}})({\bf\color{green}b_{1}}{\bf\color{orange}W^{k}_{2}} + {\bf\color{green}b_{2}}{\bf\color{orange}W^{k}_{4}}) \end{pmatrix} \]

All weights from all weight matrices attend to only the second word

Attention matrix


\[\text{Attention Matrix: } Q \cdot K^{T}=\] \[ \begin{pmatrix} a_{1}W^{q}_{1} + a_{2}W^{q}_{3} & a_{1}W^{q}_{2} + a_{2}W^{q}_{4} \\ b_{1}W^{q}_{1} + b_{2}W^{q}_{3} & b_{1}W^{q}_{2} + b_{2}W^{q}_{4} \end{pmatrix} \cdot \begin{pmatrix} a_{1}W^{k}_{1} + a_{2}W^{k}_{3} & b_{1}W^{k}_{1} + b_{2}W^{k}_{3} \\ a_{1}W^{k}_{2} + a_{2}W^{k}_{4} & b_{1}W^{k}_{2} + b_{2}W^{k}_{4} \end{pmatrix} \]

\[ = \begin{pmatrix} (a_{1}W^{q}_{1} + a_{2}W^{q}_{3})(a_{1}W^{k}_{1} + a_{2}W^{k}_{3})+(a_{1}W^{q}_{2} + a_{2}W^{q}_{4})(a_{1}W^{k}_{2} + a_{2}W^{k}_{4}) & ({\bf\color{green}a_{1}}{\bf\color{purple}W^{q}_{1}} + {\bf\color{green}a_{2}}{\bf\color{purple}W^{q}_{3}})({\bf\color{green}b_{1}}{\bf\color{orange}W^{k}_{1}} + {\bf\color{green}b_{2}}{\bf\color{orange}W^{k}_{3}}) + ({\bf\color{green}a_{1}}{\bf\color{purple}W^{q}_{2}} + {\bf\color{green}a_{2}}{\bf\color{purple}W^{q}_{4}})({\bf\color{green}b_{1}}{\bf\color{orange}W^{k}_{4}} + {\bf\color{green}b_{2}}{\bf\color{orange}W^{k}_{4}}) \\ ({\bf\color{green}b_{1}}{\bf\color{purple}W^{q}_{1}} + {\bf\color{green}b_{2}}{\bf\color{purple}W^{q}_{3}})({\bf\color{green}a_{1}}{\bf\color{orange}W^{k}_{1}} + {\bf\color{green}a_{2}}{\bf\color{orange}W^{k}_{3}})+({\bf\color{green}b_{1}}{\bf\color{purple}W^{q}_{2}} + {\bf\color{green}b_{2}}{\bf\color{purple}W^{q}_{4}})({\bf\color{green}a_{1}}{\bf\color{orange}W^{k}_{2}} + {\bf\color{green}a_{2}}{\bf\color{orange}W^{k}_{4}}) & (b_{1}W^{q}_{1} + b_{2}W^{q}_{3})(b_{1}W^{k}_{1} + b_{2}W^{k}_{3})+(b_{1}W^{q}_{2} + b_{2}W^{q}_{4})(b_{1}W^{k}_{2} + b_{2}W^{k}_{4}) \end{pmatrix} \]

All weights from all weight matrices attend to both words

Attention mechanism


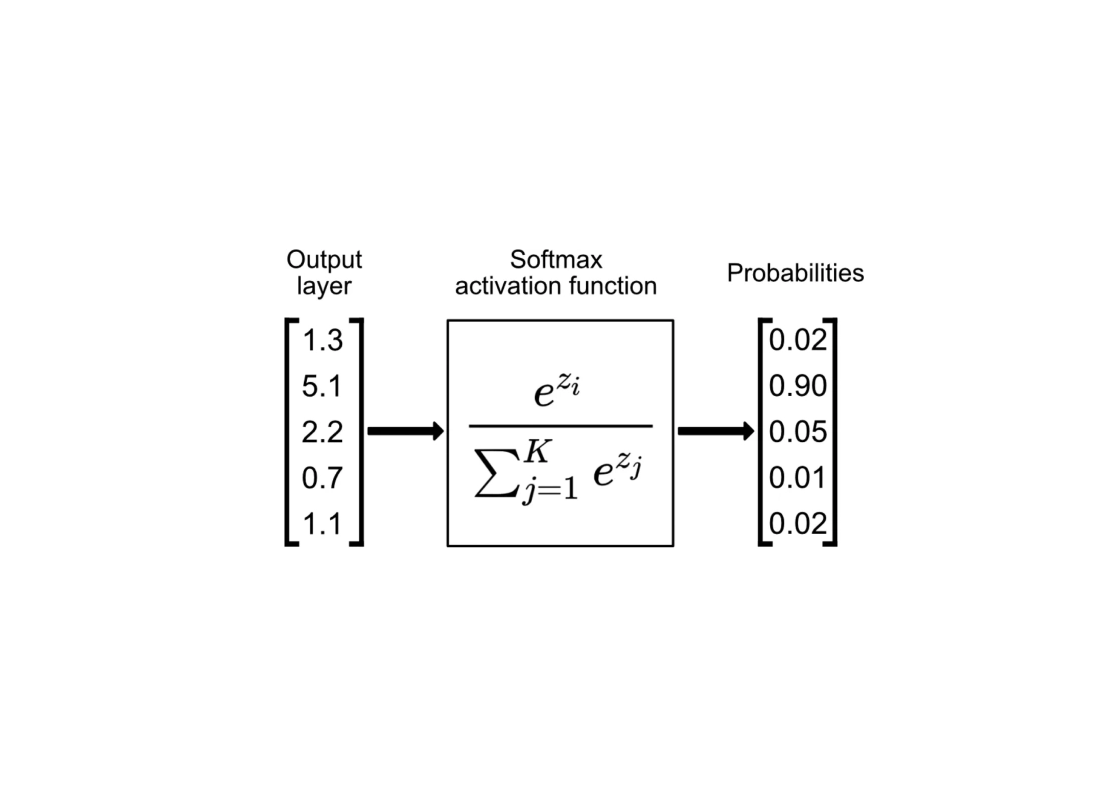
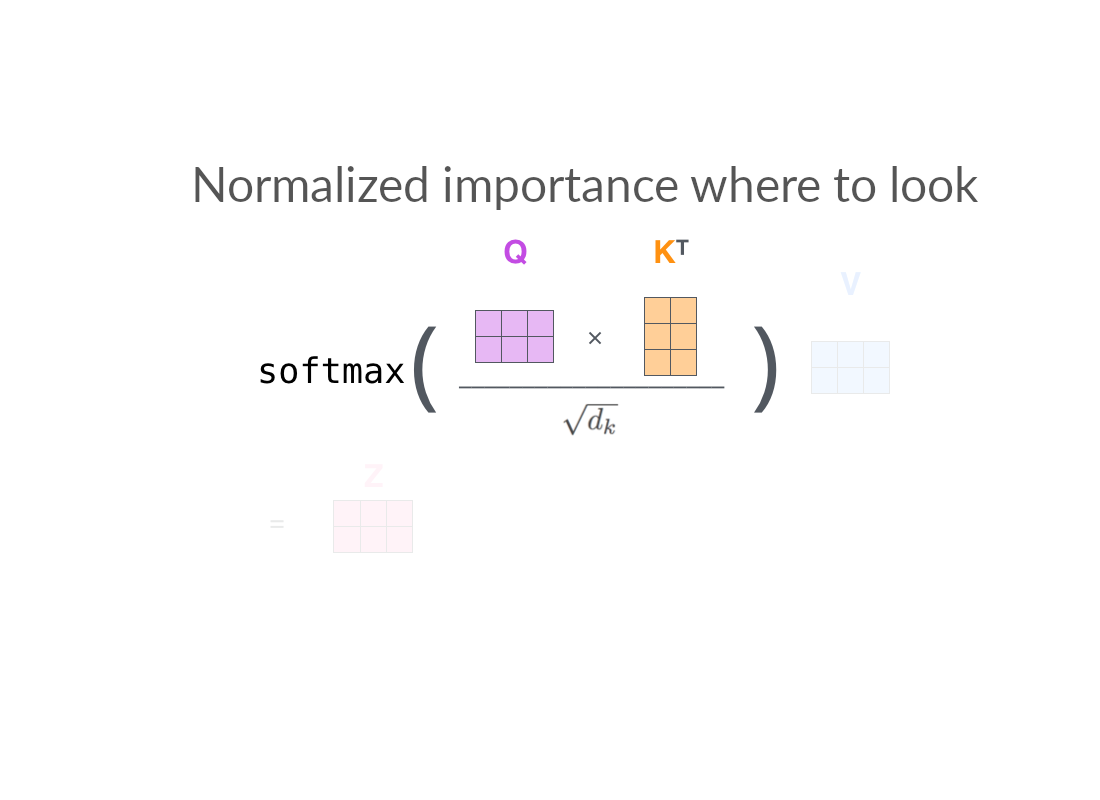
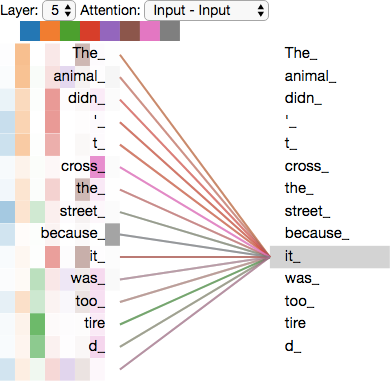
Jay Alammar - The Illustrated Transformer

An example


”The animal didn't cross the street because it was too tired”

”The animal didn't cross the street because it was too tired”

jalammar.github.io/illustrated-transformer

The original transformer



  • An encoding component
  • A decoding component
  • Connections between them
  • The attention mechanism
  • A positional encoding


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

Positional encoding

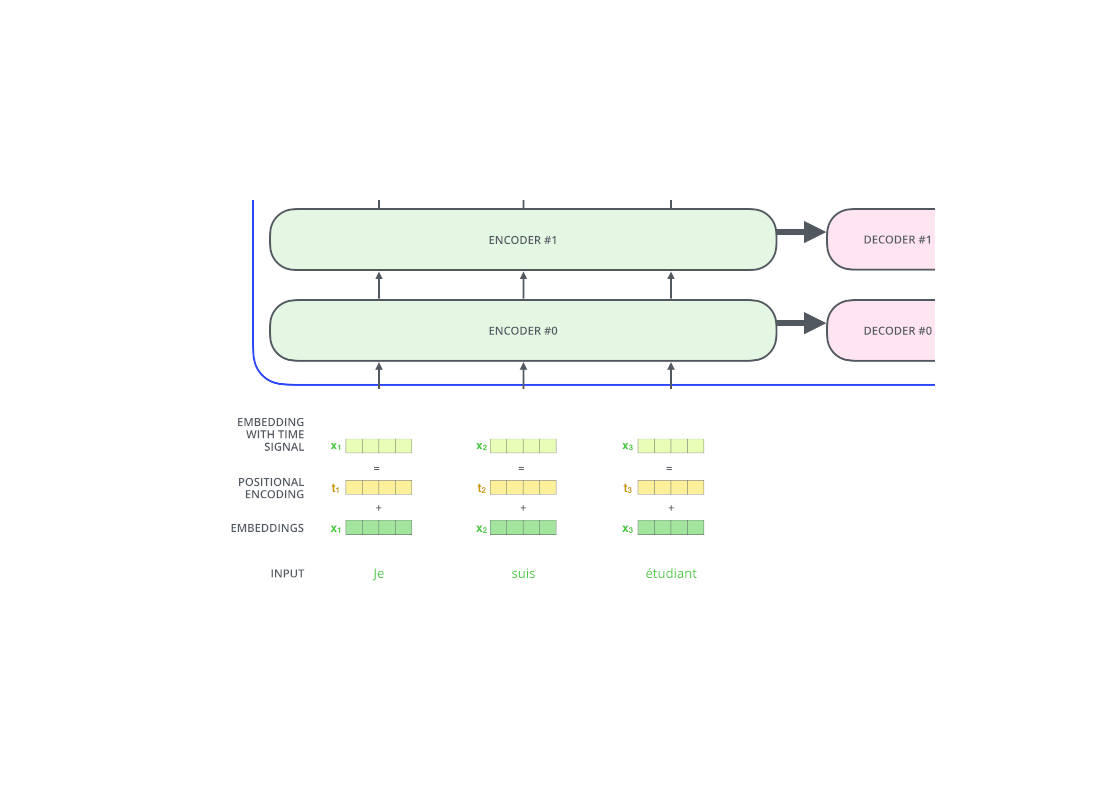
Jay Alammar - The Illustrated Transformer

The original transformer



  • An encoding component
  • A decoding component
  • Connections between them
  • The attention mechanism
  • A positional encoding
  • Residual connections


Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008

Residual connections

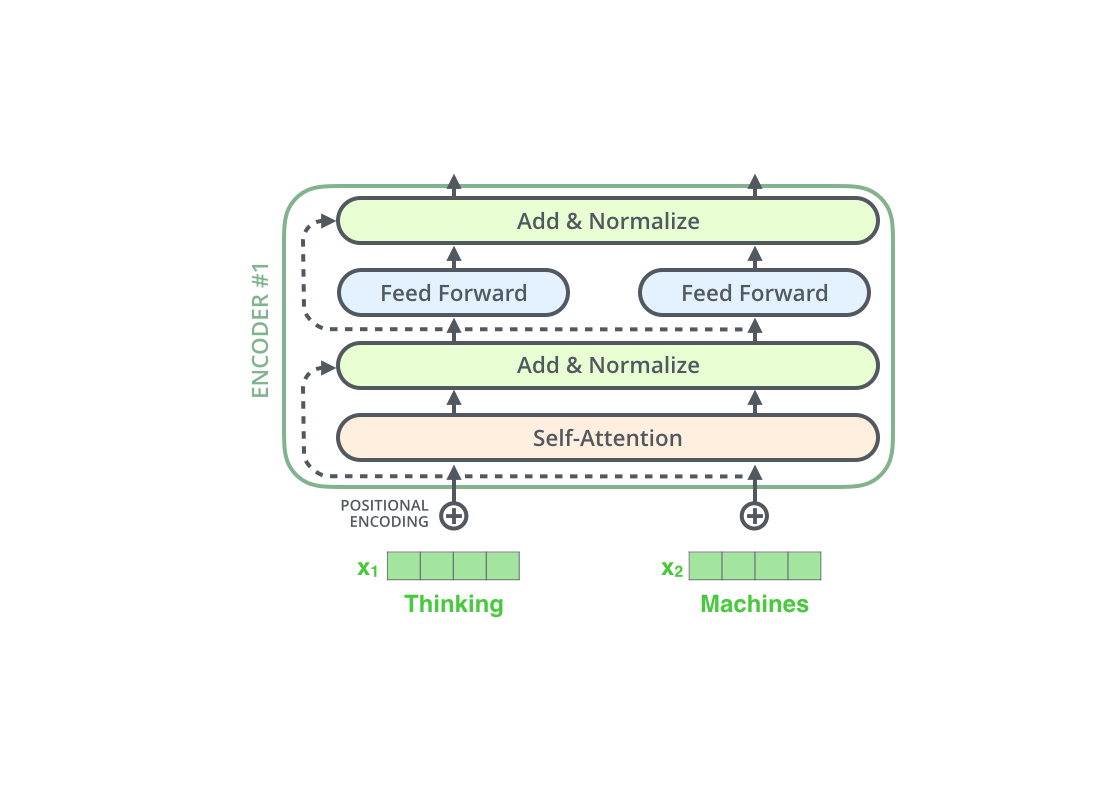
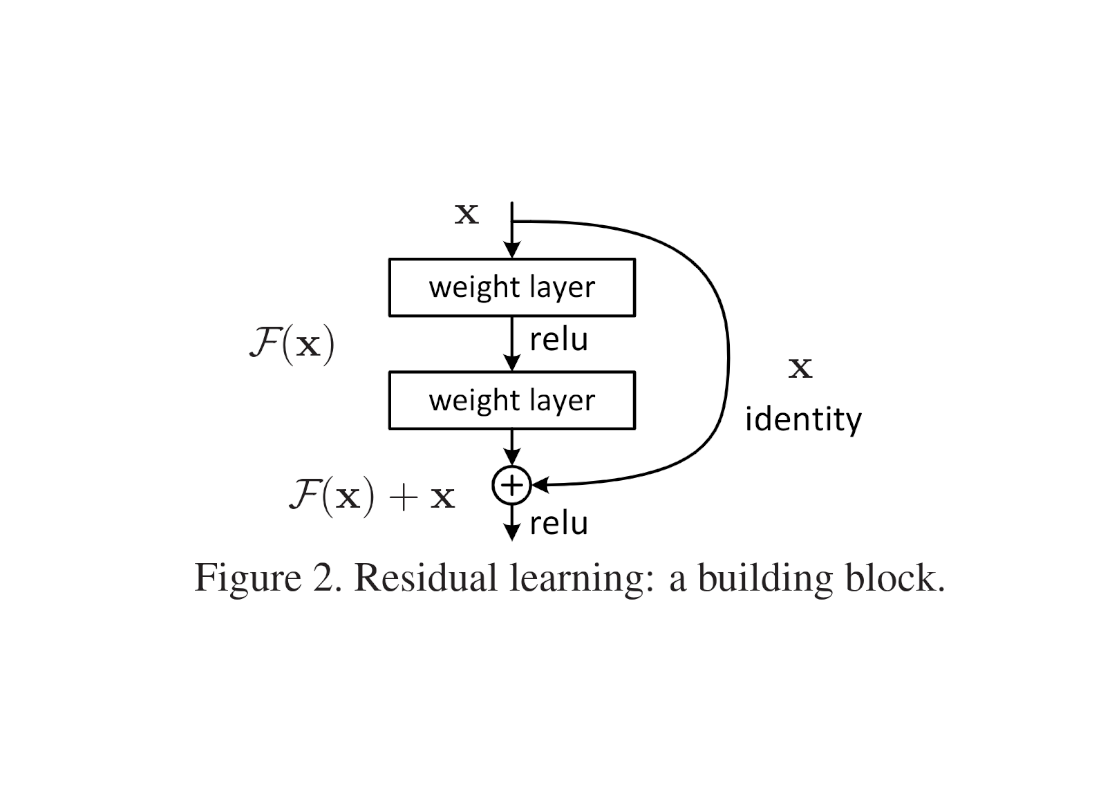
Jay Alammar - The Illustrated Transformer

He, K., et al. (2016) IEEE proceedings on computer vision and pattern recognition (pp. 770-778)

How to input data (Frontend)


Utkarsh Kant - Tokenization

Dosovitskiy, A., et al. (2020). Preprint at arxiv:2010.11929

Schäfer-Zimmermann, J. C., et al. (2024). Preprint at arXiv:2406.01253

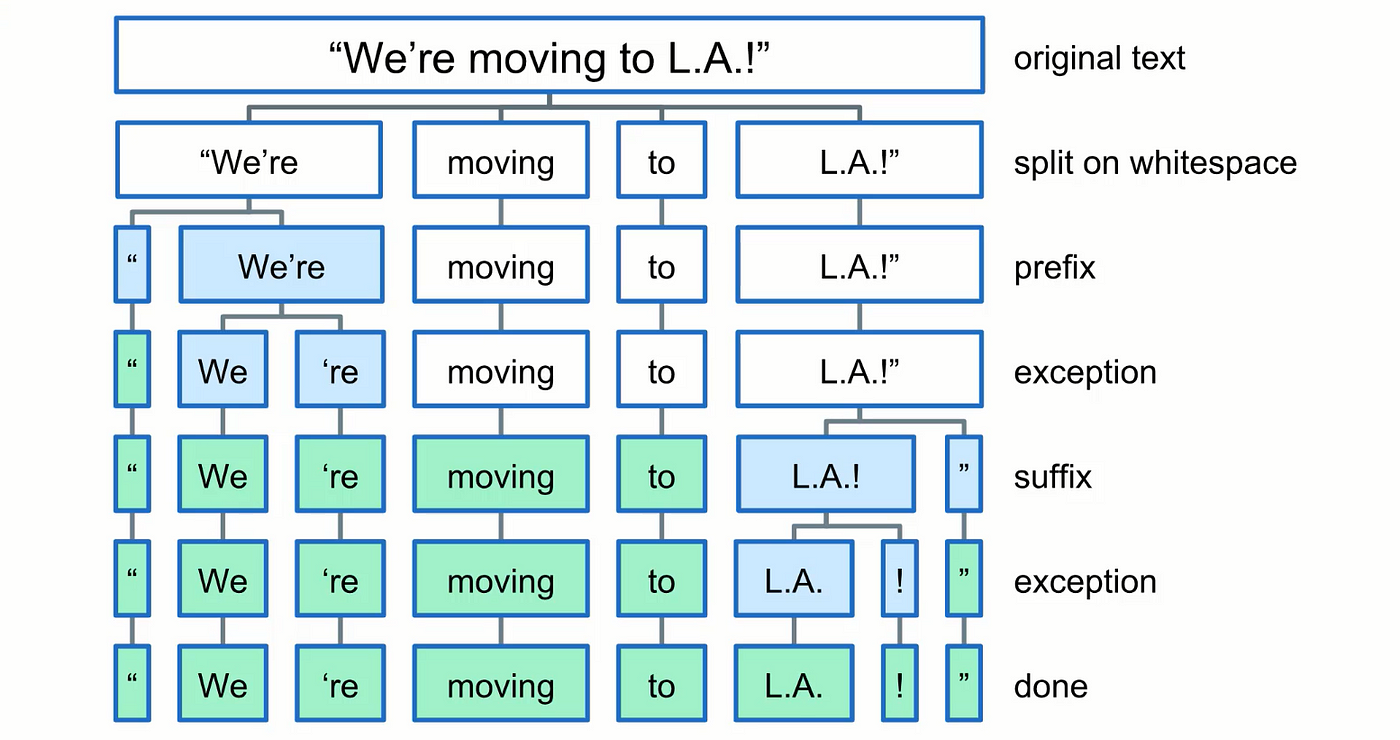
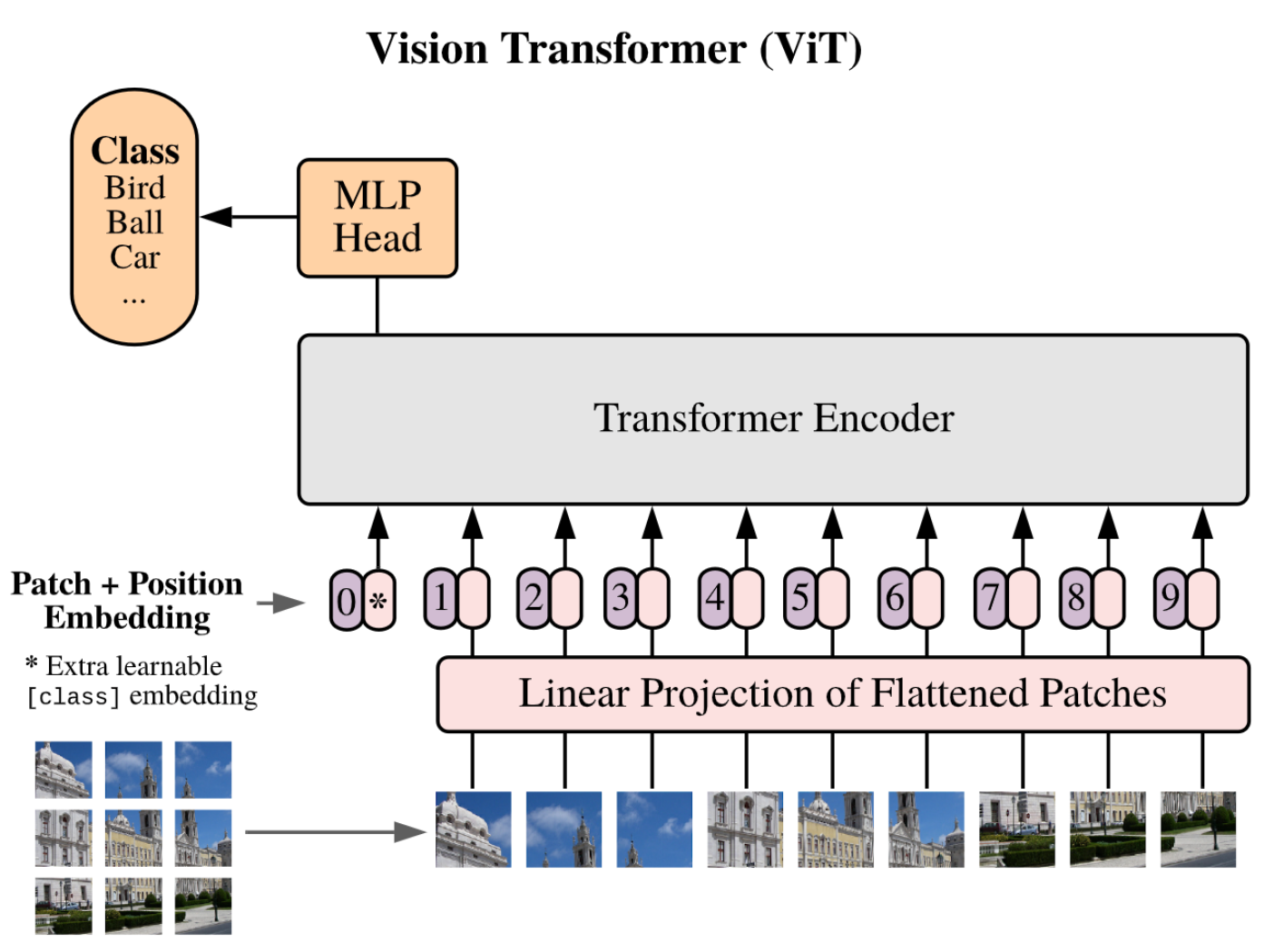
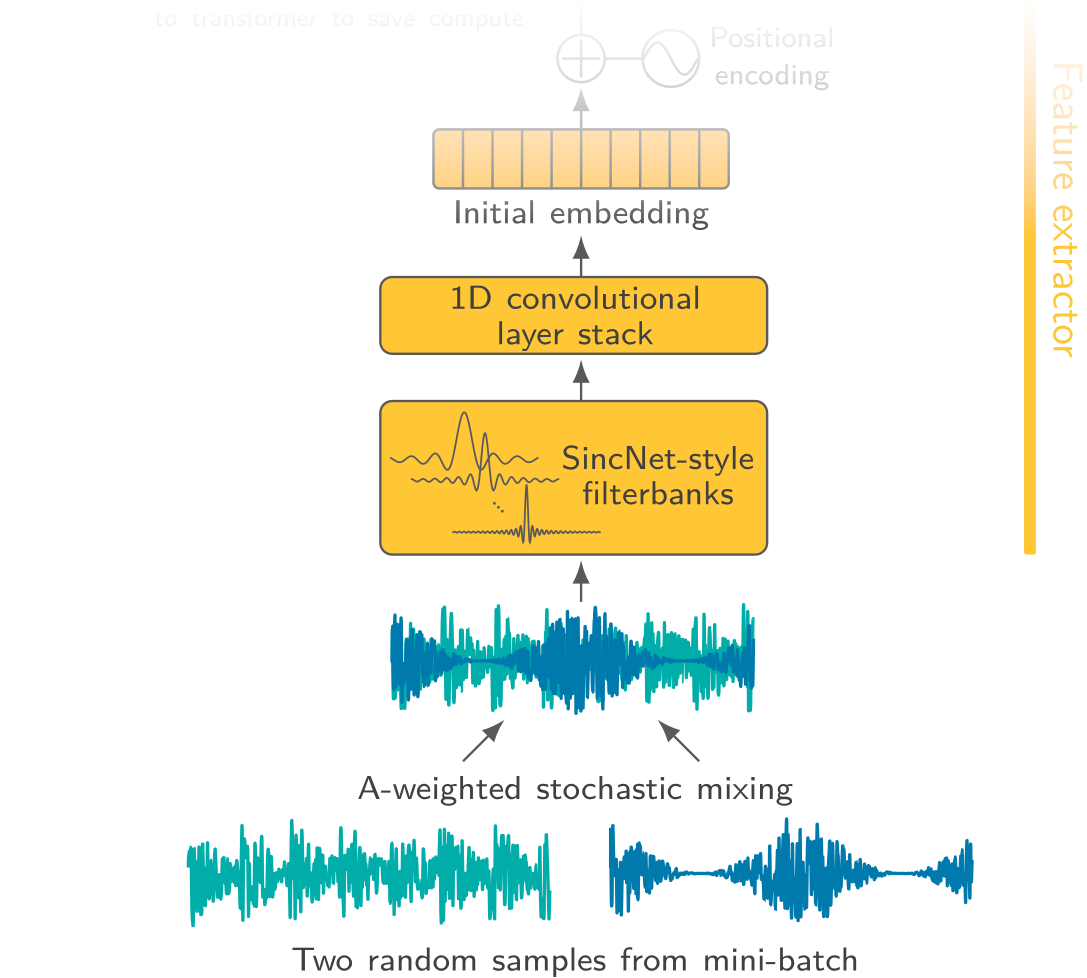
Overview



    The transformer:

  • The Swiss army knife of neural network architectures
  • Needs usually more data for convergence as no inductive bias
  • Computational complexity scales quadratically
  • State-of-the-art results (if you can afford it)
  • All foundational models (exhaustively pretrained) are transformers



Vaswani, A., et al. (2017) Advances in Neural Information Processing Systems 30, 5998–6008


Introductory talk on

Self-supervised learning and transformers

What is it and do I need it?


Julian C. Schäfer-Zimmermann


Max Planck Institute of Animal Behavior

Department for the Ecology of Animal Societies

Communication and Collective Movement (CoCoMo) Group